I investigated experiments with SPSS and following values were out.
I have a question that in which case is possible to get Feature 1 in Group A+B as significant p<.05 while either Group A and B has low significance in Feature 1?
I hardly interpret because Group A have low correlation and Group B also, but combined group have correlation with (very) high significance.
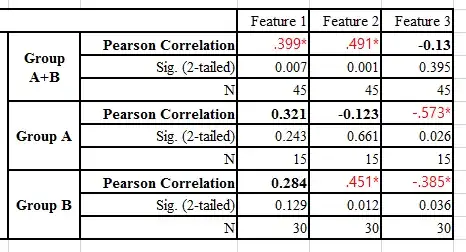
(* p<.05)