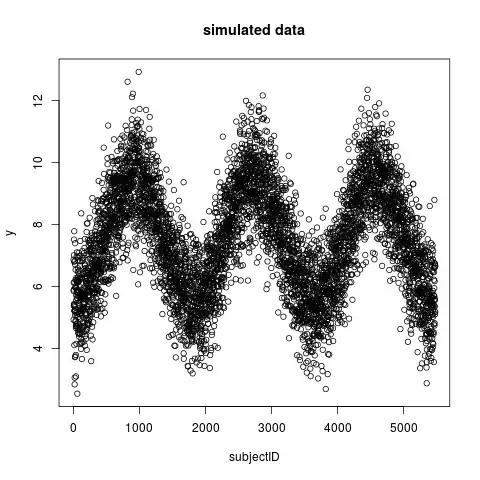
I simulated data a bit like yours, three years of daily data, 5 samples per day.
set.seed(42)
ts <- seq(as.POSIXct('2012/1/1 00:00'), as.POSIXct('2014/12/31 23:59'), 'days')
ts <- rep(ts, each=5) ## 5 samples every day
n <- length(ts)
and generated a response by adding noise to a - b * cos(t):
y <- 7.5 + -2 * cos(seq(n)*2*pi/(365*5)) + rnorm(n,0,1)
The data have roughly the range and mean of yours, with a strong seasonal signal:
Form a data frame based on integer values and generate a month index:
d <- data.frame(sid=seq(n), month=as.POSIXlt(ts)$mon+1, y=round(y))
head(d)
sid month y
1 1 1 7
2 2 1 5
3 3 1 6
4 4 1 6
5 5 1 6
6 6 1 5
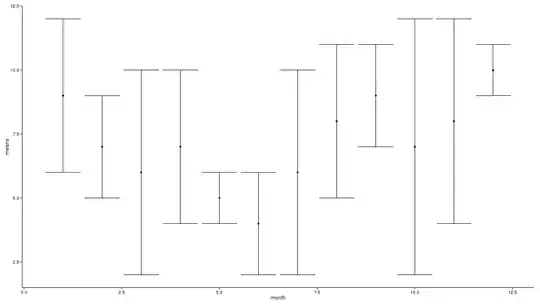
Plot the response by month:
boxplot(y~month, data=d, xlab='month', ylab='y', main='simulated data')

This is roughly similar to your own, with a seasonal signal both stronger and clearer.
Fit a very simple linear model with separate means for each month:
fit <- lm(y ~ factor(month), data=d)
summary(fit)
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 5.57419 0.04957 112.453 < 2e-16 ***
factor(month)2 0.47287 0.07173 6.592 4.74e-11 ***
factor(month)3 1.37849 0.07010 19.664 < 2e-16 ***
factor(month)4 2.41935 0.07010 34.512 < 2e-16 ***
factor(month)5 3.35054 0.07010 47.796 < 2e-16 ***
factor(month)6 3.86358 0.07068 54.661 < 2e-16 ***
factor(month)7 3.83871 0.07010 54.759 < 2e-16 ***
factor(month)8 3.23226 0.07010 46.108 < 2e-16 ***
factor(month)9 2.34358 0.07068 33.156 < 2e-16 ***
factor(month)10 1.35692 0.07068 19.197 < 2e-16 ***
factor(month)11 0.58803 0.07068 8.319 < 2e-16 ***
factor(month)12 -0.01075 0.07010 -0.153 0.878
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 1.069 on 5468 degrees of freedom
Multiple R-squared: 0.633, Adjusted R-squared: 0.6323
F-statistic: 857.4 on 11 and 5468 DF, p-value: < 2.2e-16
The output here assumes January as a reference month and bundles the January mean with the intercept term. The significance of the individual month
factors are then interpreted as "is the mean for this month significantly different to January?". For these data, all months are significantly different to January, except December. December and January are (statistically) indistinguishable from one another. One interpretation of this is that there is a seasonal difference between (southern hemisphere) summer months and the rest of the year.
This is not a great model by any stretch of the imagination. It doesn't even do a spectacular job at estimating the true simulated mean of 7.5. There are many shortcomings and criticsms that could be made. Importantly, it doesn't account for correlations in response between adjacent months, for example. It does, however, satisfy your initial criteria of answering the question about significant time-varying structure and reporting p-values. It's crude but "good enough" to detect a seasonal difference (in these data, even after a lot of detail has been lost to month binning). Any refinement to the correlation structure will only enhance it's sensitivity.
The point is not to defend this particular model but to say: any model you fit will have shortcomings. Finding an appropriate model for your needs depends on you having clear ideas about the goals of the analysis and the context in which it will be evaluated.
As @Nick Cox, @IrishStat (and others) have pointed out, there are many things that could be done here, almost all of them more sophisticated than this approach. But it is difficult to know what to suggest without a clear idea of what you aim to achieve. The question "Does the variable have a significant seasonal variation?" is not focused enough to guide the choice of model framework. In some contexts sARIMA may be warranted, in others the above may be adequate.
I hope that helps.