10

A lot of statistics textbooks provide an intuitive illustration of what the eigenvectors of a covariance matrix are:

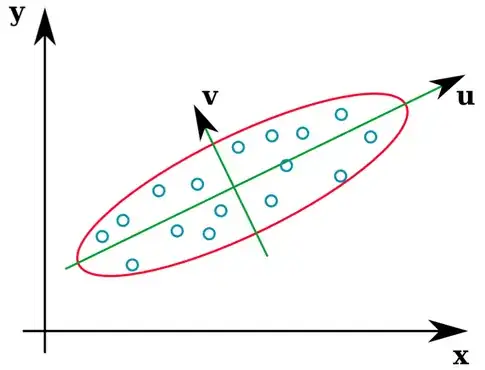
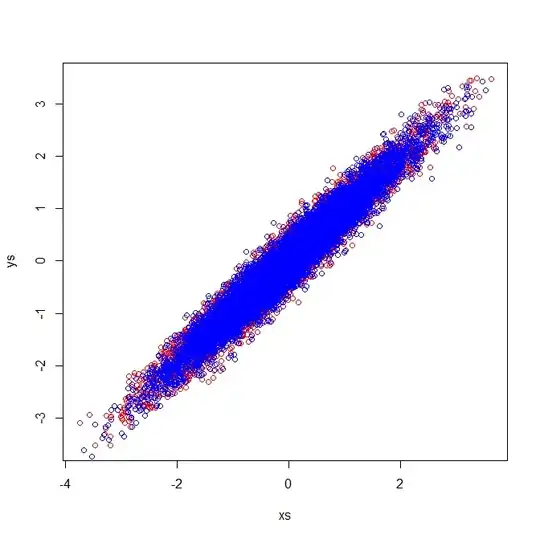
enter image description here

The vectors u and z form the eigenvectors (well, eigenaxes). This makes sense. But the one thing that confuses me is that we extract eigenvectors from the correlation matrix, not the raw data. Furthermore, raw datasets that are quite different can have identical correlation matrices. For example, the following both have correlation matrices of:

$$\left[\begin{array}{} 1 & 0.97 \\ 0.97 &1\end{array}\right]$$

Eigenvectors

As such they have eigenvectors pointing in the same direction:

$$\left[\begin{array}{} .71 & -.71 \\ .71 & .71\end{array}\right]$$

But if you were to apply the same visual interpretation of which directions the eigenvectors were in the raw data, you would get vectors pointing in different directions.

Can someone please tell me where I have gone wrong?

Second Edit: If I may be so bold, with the excellent answers below I was able to make sense of the confusion and have illustrated it.

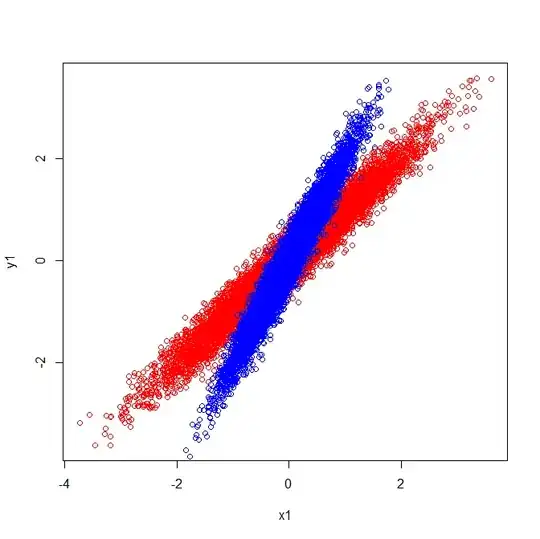
  1. The visual explanation coheres with the fact that the eigenvectors extracted from the covariance matrix are distinct.

    Covariances and Eigenvectors (Red):

    $$\left[\begin{array}{} 1 & 1 \\ 1 & 1\end{array}\right] \left[\begin{array}{} .7 & -.72 \\ .72 & .7\end{array}\right]$$

    Covariances and Eigenvectors (Blue):

    $$\left[\begin{array}{} .25 & .5 \\ .5 & 1\end{array}\right] \left[\begin{array}{} .43 & -.9 \\ .9 & .43\end{array}\right]$$

  2. Correlation matrices reflect the covariance matrices of the standardized variables. Visual inspection of the standardized variables demonstrate why identical eigenvectors are extracted in my example:

enter image description here

gung - Reinstate Monica
  • 132,789
  • 81
  • 357
  • 650
Sue Doh Nimh
  • 719
  • 4
  • 20
  • 3
    If you wish to evaluate *correlation*, then you must draw your scatterplots with scales in which the standard deviations of the components are equal. That is not the case in any of your images (except perhaps for the red dots in the second one), which may be one reason you find this confusing. – whuber Nov 17 '14 at 21:24
  • 3
    I appreciate your having illustrated your question. That helps people understand it & adds to the value of the thread for future reference. Be aware, however, that ~10% of men are red-green colorblind. With 2 colors, red & blue may be safer. – gung - Reinstate Monica Nov 17 '14 at 21:42
  • Many thanks, I have corrected the colors as you suggested – Sue Doh Nimh Nov 17 '14 at 22:25
  • 2
    No problem, @SueDohNimh. Thank you for making it intelligible for all. On a different note, I would keep the `[PCA]` tag. If you want to re-focus the question, or ask a new (related) question & link to this one, that seems fine, but I think this question is PCA-ish enough to merit the tag. – gung - Reinstate Monica Nov 17 '14 at 22:36
  • Nice job, @SueDohNimh. You could also add that as an answer to your own question instead of an edit, if you wanted to. – gung - Reinstate Monica Nov 18 '14 at 00:05

1 Answers1

9

You don't have to do PCA over the correlation matrix; you can decompose the covariance matrix as well. Note that these will typically yield different solutions. (For more on this, see: PCA on correlation or covariance?)

In your second figure, the correlations are the same, but the groups look different. They look different because they have different covariances. However, the variances are also different (e.g., the red group varies over a wider range of X1), and the correlation is the covariance divided by the standard deviations (${\rm Cov}_{xy} / {\rm SD}_x{\rm SD}_y$). As a result, the correlations can be the same.

Again, if you perform PCA with these groups using the covariance matrices, you will get a different result than if you use the correlation matrices.

Community
  • 1
gung - Reinstate Monica
  • 132,789
  • 81
  • 357
  • 650
  • 2
    +1 You have probably also noticed that with two variables the correlation matrix always has the same two eigenvectors, $(1,1)$ and $(1,-1)$, *no matter what value the correlation has.* – whuber Nov 17 '14 at 21:33
  • 1
    +1 to what @whuber wrote, but note that the corresponding eigenvalues do depend on the correlation value. – amoeba Nov 17 '14 at 21:41
  • This is true, but the eigenvectors of the Cov matrix can vary based on the correlation. – gung - Reinstate Monica Nov 17 '14 at 21:57
  • And another thread http://stats.stackexchange.com/q/62677/3277 – ttnphns Nov 17 '14 at 21:59
  • 1
    Hi guys, many thanks. I was aware that distinct eigenvectors arise from using the covariance matrices instead; this was a further source of concern as I made me worry that by using correlation matrices instead I was reducing the information being used and therefore being less accurate. Would it be sensible to conclude based on your responses that the visual interpretation provided is only really applicable to eigenvectors of the covariance matrix of the raw data rather than the correelation matrix? – Sue Doh Nimh Nov 17 '14 at 22:29
  • 1
    Not really, @SueDohNimh. You can use the visual interpretation, just standardize your variables first if you want to use the correlation matrix. – gung - Reinstate Monica Nov 17 '14 at 22:33