4

Suppose we have the following model for the variable $V_5$: $$V_5 = \prod_{k=1}^5(e^{\mu + 0.2X_k}+0.05e^{0.05Y_i - 0.00125}), X_i,Y_i\sim N(0,1)$$

What I wish to do is to solve the problem $\min_{\mu}\{F_{V_5}(1.2763) = 0.25\}$. By performing $10^7$ simulations for the value of $V_5$, I find that this optimal $\mu$ is somewhere in the neighborhood of $0.06$ with small deviations in the value of $F$, i.e. I find that if $\mu = 0.06$ then $F_{V_5}(1.2673) = 0.2484$ or $0.2487$ or other very similar values in that area, but never exactly $0.25$. If I change the value of $\mu$ to either larger or smaller than $0.06$ then the value of $F$ starts diverging farther away from $0.25$. In addition, the empirical CDF is clearly not normal, but it does approximate a normal with mean the sample mean of $V_5$ and $\sigma^2$ the sample variance of $V_5$ rather closely at exactly the point $(1.2763 , 0.25)$ as you can see in the picture below (and I'm not sure that this is a coincidence or not):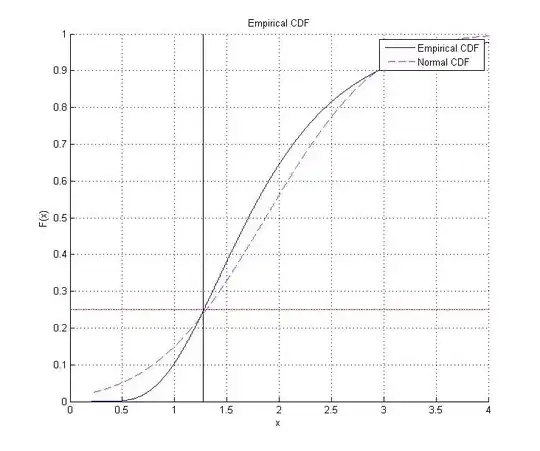enter image description here

Now my question is, how can I prove that $\mu = 0.06$ is indeed the optimal value that we are looking for? When I asked my professor, he said that I should construct a confidence interval, but since we didn't get $\mu$ from an estimation or anything (I found it by rather eyeballing the problem), that leaves me with the idea of a confidence interval for the probability $F_{V_5}(1.2763)$, which I have no clue how to construct.

Any suggestion or different solution to the problem is most welcome.

Firebug
  • 15,262
  • 5
  • 60
  • 127
Emil
  • 1,003
  • 1
  • 8
  • 12
  • What does "$F_{V_5}$" mean? Would it be the CDF of $V_5$? Since $V_5$ is defined entirely by formulas, what do you mean by "empirical" CDF and "confidence interval"? Are there data for $V_5$ available somewhere? – whuber Nov 17 '14 at 19:12
  • $F_{V_5}$ is the empirical CDF of $V_5$, meaning it is the CDF based on the values of $V_5$ that were produced by the simulations. The data for $V_5$ are therefore simulated, not somewhere on the internet (if I understood your question correctly). – Emil Nov 17 '14 at 19:18
  • A confidence interval based on a simulation has little or no meaning: you could shorten it arbitrarily merely by running the simulation longer. It is difficult to see in any case how a CI could "prove" that $0.06$ is the optimal value of $\mu$, because it is a statement about the *simulation*, not about $\mu$! So are you really just asking how to find the (smallest) value of $\mu$ for which the $0.25$ quantile of $V_5(\mu)$ is equal to $1.2763$? – whuber Nov 17 '14 at 19:22
  • 1
    Yes, that is exactly what I am trying to do. The problem is that I didn't reach the numerical value of $0.06$ analytically (and I don't think that can be achieved because the distribution of $V_5$ is rather complicated to compute). Therefore, I don't know how to justify that $0.06$ is indeed the correct value. – Emil Nov 17 '14 at 19:35

1 Answers1

0

Let $$U = \log(e^{\mu + 0.2X}+0.05e^{0.05Y - 0.00125})$$ where $X$ and $Y$ are standard normals. Then approximately $$\log(V_5) \sim N\left(5 E[U],\sqrt{5 Var[U]}\right)$$ since adding five approximately-normal variables gives a variable which is even closer to normal.

So the first quartiles of these variables are also approximately equal, and for the desired $\mu$ this yields: $$\log(1.2763) \simeq 5E[U] - 0.6745\sqrt{5 Var[U]}$$

To solve this, we write $U$ as a Taylor series in $\mu$: $$U = \log(e^{0.2X}+0.05e^{0.05Y - 0.00125}) + \frac{e^{0.2X}\mu}{e^{0.2X}+0.05e^{0.05Y - 0.00125}} + O(\mu^2)$$ from which we conclude $$E[U] = 0.04970 + 0.95156\mu + O(\mu^2)$$ $$Var[U] = E[(U-E[U])^2] = 0.03623 + 0.003487\mu + O(\mu^2)$$ Substituting those in the equation above, we find that $\mu = 0.05955$ to a good degree of approximation, and Taylor series with more terms would give $\mu = 0.05947$.

Matt F.
  • 1,656
  • 4
  • 20