3

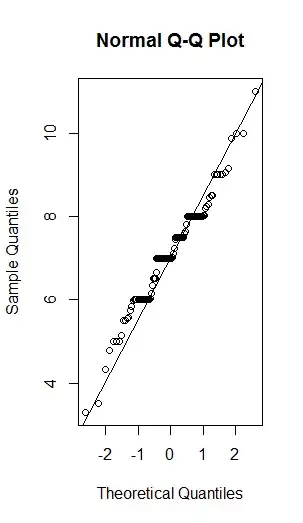
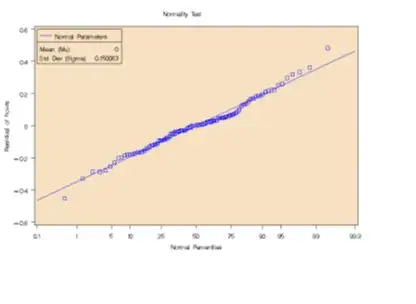
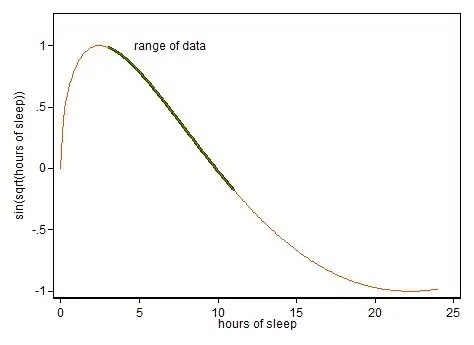
I need to perform a two-way ANOVA on my data ($Y$: sleeping hours). My data is quite normal $p$-value = $0.07$ with Shapiro-Wilk test but when I run the normality test for my residual, $p$-value is less than $0.01$. So I did the transformation by using $f(x) = \sin(\sqrt{x})$. My new normality test for residual from coded data is 0.03. My question is

  1. Is $\alpha = 0.03$ enough for the normality test to perform two-way ANOVA? I have tried $\ln(x)$, $\sin(x)$, inverse, $\sqrt{x}$, but they are all worse.
  2. What does $f(x) = \sin(\sqrt{x})$ really do to my data?

Raw data Coded data: residual plot

Nick Cox
  • 48,377
  • 8
  • 110
  • 156
Phume
  • 75
  • 6
  • 1
    Sleeping hours is presumably a number with a mean around 7 if these are human adults and something positive otherwise. The first seems borne out by your first plot. But arc sin square root is a transformation applicable to proportions in $[0,1]$. So, it's not at all clear what you did. If you scaled sleeping hours to fraction of day, that's better, but "sleeping hours" is then a poor name for the variable. If you applied arc sin square root to numbers like 7 to software that expects percents, then that's wrong in principle, although by accident not completely wrong in terms of what it does. – Nick Cox Nov 16 '14 at 16:15
  • 4
    The standard transformation is arcsin$(\sqrt x)$, i.e. the inverse of the sine function, not the sine. – Nick Cox Nov 16 '14 at 16:21
  • I know it supposed to be $arcsin(\sqrt{x})$ but $sin(\sqrt{x})$ works way better. – Phume Nov 16 '14 at 18:39
  • @Nick Cox. I know it's wrong in principle, that's why I ask this question. The range of my data is [4,10] hours. After the transformation, the range becomes [-.02,0.7]. – Phume Nov 16 '14 at 18:41
  • Wrong in principle is an understatement. My first two comments make clear that I thought you were applying arcsin(root()) to numbers **as if** they were percents. What you have apparently done using sin(root()) is even more bizarre. – Nick Cox Nov 16 '14 at 18:57
  • 6
    You can't expect to throw random transformations at data and have it make any sense at all. – Glen_b Nov 16 '14 at 23:01

2 Answers2

11

I still don't understand exactly what you did, but here is a plot of sin(sqrt(hours of sleep)) over the approximate range observed and between the absolute limits of 0 and 24 hours.

By accident the transformation is monotonic for the observed range, although almost linear, so the effect on the distribution should be slight.

It is quite absurd otherwise. It has no basis theoretically.

In terms of the bigger question, it's not clear to me that the distribution of the data is awkward for ANOVA at all.

EDIT Small print: Your first graph I read as showing data from about 3 to about 11 hours, you say you have 4 to 10 and transformed you have 0.7 to -0.02. But although sin(root(10) is about -0.02, sin(root(4)) is about 0.91. So there are small contradictions here. Regardless of that, this transformation is indefensible, as it is not even monotonic over the possible range.

enter image description here

Nick Cox
  • 48,377
  • 8
  • 110
  • 156
  • What do you mean by "it's not clear to me that the distribution of the data is awkward for ANOVA at all"? – Phume Nov 16 '14 at 19:57
  • 3
    Phume - there's no obvious reason why there would be a problem using anova on your data; there's some discreteness, which might be enough for the Shapiro-Wilk to reject on such a large sample, but so what (since when are real data exactly normal)? What is it about your data that make them unsuitable for anova? – Glen_b Nov 16 '14 at 23:02
  • Glen_b - It make ANOVA test unstable because my residuals is not normally distributed since p-value < 0.01 form kolmogorov-smirnov test. – Phume Nov 17 '14 at 01:38
5

Nick Cox has done a good job talking about the transformation of your data. Let me address some other issues in your question.

You state that your data are "quite normal" because the $p$-value from a Shapiro-Wilk test is $.07$. There are several problems here. First, the distribution of your data is irrelevant; only the distribution of the residuals is important. (To understand this more fully, see: What if the residuals are normally distributed, but y is not?) Second, there is no 'bright line' at $.05$. $.07$ is pretty close to $.05$, and unless you powered your study to reject normality at a specific level of $W$ for some reason, I would say that is enough to be called 'significant'. (For more on this, see my answer here: When to use Fisher & Neyman-Pearson framework?, also this quote.) Moreover, the normal distribution is just a mathematical idealization, no data are ever really normal (quote). In particular, your data can't be $<0$ and shows evidence of rounding; with enough data, there is no question you would get a $p$-value $<.05$ (cf.: Is normality testing 'essentially useless'?).

Community
  • 1
gung - Reinstate Monica
  • 132,789
  • 81
  • 357
  • 650
  • 3
    +1. It looks as if your dataset is sufficiently small to post here. People would be quite likely to offer ideas on analysis if they could play with the data. – Nick Cox Nov 17 '14 at 00:46