2

I know in studies where relative risk or odds ratio is calculated, if confidence interval overlaps 1, then the P-value is not significant. Is similar relation true for following situations as well?

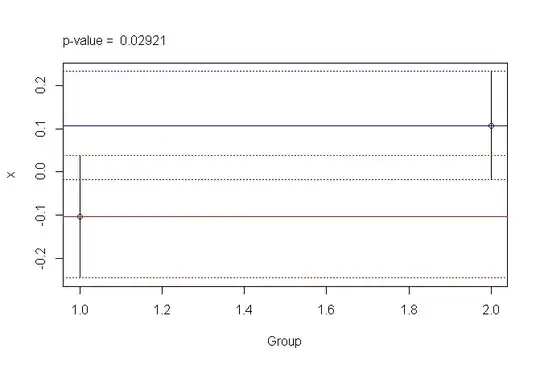
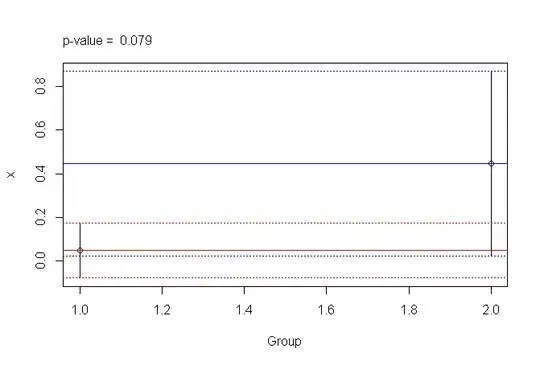
Consider 2 sets of values with means m1 and m2. I think, if 95% confidence intervals of m1 and m2 are not overlapping, then the p-value for an unpaired t-test comparing them will yield P<0.05, indicating that they are not from same population. Is this true?

Or does one need only to check if m2 lies outside the 95% confidence intervals of m1 (or m1 lies outside 95% confidence intervals of m2), then the p-value of unpaired t-test between 2 sets will yield P<0.05?

Thanks for your insight.

Edit: A corollary of above (as discussed in the comments) is that if notches of 2 boxplots do not overlap, there must be a significant difference between the them.

rnso
  • 8,893
  • 14
  • 50
  • 94

1 Answers1

3

Do not use this overlapping criterion because it's not exactly fool-proof. Sometimes the two intervals can overlap and yet the mean difference is statistically significant (p-value is taken from t-test):

enter image description here

And sometimes one of the means can be excluded from the other group's interval and yet the difference is not statistically significant:

enter image description here

So, there can be weird exceptions. The equivalent statistics you are looking for is the mean difference and its 95% CI. If that interval contains 0, then the p-value will be bigger than 0.05.

Penguin_Knight
  • 11,078
  • 29
  • 48
  • Thanks for a very well illustrated explanation. So the concept that if notches of two boxplot do not overlap, their difference MUST be significant, is incorrect, though difference is LIKELY to be signficant. http://docs.ggplot2.org/0.9.3.1/geom_boxplot.html – rnso Nov 17 '14 at 03:22
  • @rnso, boxplot notches are for median, not mean. But yes, lack of overlapping strongly suggests the medians being different, but probably not 100%. – Penguin_Knight Nov 17 '14 at 03:29
  • Found 2 other posts on this issue: https://stats.stackexchange.com/questions/262495/reading-box-and-whisker-plots-possible-to-glean-significant-differences-between and https://stats.stackexchange.com/questions/228719/box-plot-notches-vs-tukey-kramer-interval – rnso Nov 18 '18 at 15:44
  • @Penguin_Knight under what conditions and assumptions is this overlapping criterion going to work / not work ? What is the intuition behind this ? – Xavier Bourret Sicotte Jul 19 '19 at 18:20