9

[This question is related to 1 and 2 on this site.]

I fit a Cox model with these three time dependent variables: {s:numeric, C:binary, l:numeric }. I have 1069 events and around half of that in right censored observations.

model<- coxph( Surv(start, stop, event) ~ s+ C+  l, data=dat)
                    coef exp(coef) se(coef)    z p
s                   3.32     27.61   0.0825 40.2 0
CTRUE               1.36      3.88   0.1086 12.5 0
l                   0.08      1.08   0.0077 10.4 0

Likelihood ratio test=990  on 3 df, p=0  n= 798431, number of events= 1069

I check the proportional hazards (PH) assumption for variables and the global model: 

cox.zph(model)
                       rho  chisq        p
s                   0.2066 12.536 0.000399
CTRUE               0.0453  2.212 0.136984
l                   0.0461  0.835 0.360842
GLOBAL                  NA 14.684 0.002108

I can see that s violates the PH assumption, resulting in strong evidence of non-proportional hazards for the global model.

Also from the plots below, which show the estimated regression coefficients as functions of time, I see that the coefficients for s looks suspicious, especially the section I circled in red:

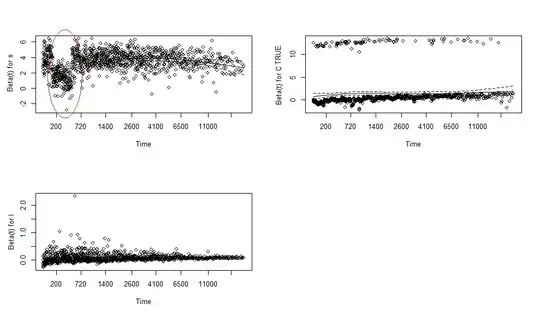
enter image description here

To treat this, I add a time interaction with s and refit the model. However, if you look at these new results, the p value for the s:stop coefficient is higher than my cut-off p= 0.05, so not statistically significant(!) :

model2<- coxph( Surv(start, stop, event) ~ s+ s:stop + C+  l, data=dat)
                        coef exp(coef) se(coef)     z     p
s                   3.25e+00     25.84 9.32e-02 34.89 0.000
CTRUE               1.36e+00      3.88 1.09e-01 12.49 0.000
l                   7.98e-02      1.08 7.72e-03 10.34 0.000
s:stop              4.42e-05      1.00 2.63e-05  1.68 0.094

Likelihood ratio test=993  on 4 df, p=0  n= 798431, number of events= 1069

Question 1: Can someone help me interpret the Schoenfeld graphs I plotted, especially what the red region in the s plot menas?

Question 2: Any general ideas on what is going on here as far as s is concerned?

P.S: I am reading the paper* below in the mean time to get a better insight but any answers by the more experienced will be very valuable.

*Patricia M Grambsch and Terry M Therneau."Proportional hazard tests and diagnostics based on weighted residuals", Biometrika, 81:515-526, 1994.

EDIT:

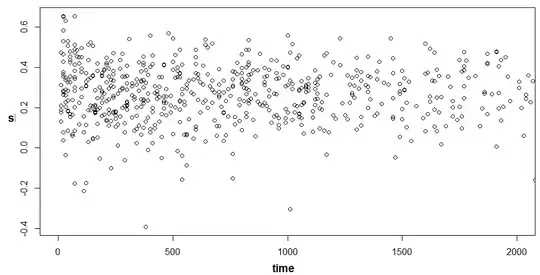
As per @EdM's comment, I plotted the s values per event time, zooming on in between the time=150 - time=700 region. Nothing particularly suspicious. So the actual s values seem normal but the coefficients the fit gives them are rather strange.

enter image description here

Community
  • 1
Zhubarb
  • 7,753
  • 2
  • 28
  • 44
  • 1
    Have you looked more closely at the data for cases that had events around the "suspicious" times (approx. times 150 to 600)? Looks like there is some systematic problem there. The straightforward "interpretation" would be that, for some reason, `s` has its major influence on event probability at early times (<150) or at late times (>600). There might be some interesting reason for this behavior, but first make sure the data are clean. – EdM Nov 13 '14 at 18:21
  • @EdM, thank you. Good advice, pls check my Edit to the question. The `s` values seem normal, it is more their Cox model coefficients that go crazy in that interval... – Zhubarb Nov 14 '14 at 09:03
  • If your data are clean, then you have to go back to the nature of the phenomenon you are investigating (which isn't stated in your question). Is there some reason why the influence of `s` on the probability of an "event" might be different at different times? Also, is there maybe some weird behavior with respect to the distribution of censoring times? – EdM Nov 14 '14 at 18:59
  • The interaction should be with the start and not the stop variable – Max Gordon Nov 25 '14 at 17:03
  • @Max Gordon, Can you explain why? In this [paper](http://cran.r-project.org/doc/contrib/Fox-Companion/appendix-cox-regression.pdf), the author applies it to `stop` on Pg. 12. I was following his example. Why should it not be applied to `stop`? – Zhubarb Nov 26 '14 at 08:22
  • @Zhubarb: I've seen that paper and I think it is a minor mistake. The basic idea is that we split the time into short periods. The start time is completely independent of what will happen later on, while the stop time will be related to the later event. This effect may be considerable if you don't split your time into small chunks. You will for instance find that any variable interacting with time has a high significance if you don't split the dataset, it is therefore easy to argue that this effect remains for the splitted dataset if you model against the stop-time instead of the start-time. – Max Gordon Nov 26 '14 at 11:32

1 Answers1

3

I think you've presented your question very well. I often use the extended Cox model (with time-varying covariates) and I've been struck by the same obstacles several times.

Like you pointed out:

cox.zph(model)
                       rho  chisq        p
s                   0.2066 12.536 0.000399
CTRUE               0.0453  2.212 0.136984
l                   0.0461  0.835 0.360842
GLOBAL                  NA 14.684 0.002108

Your model violates the PH assumption; the model as a whole violates it due to the marked violation of the s variable.

Then you show us this plot: enter image description here

I rarely bother to assess the plots if my cox.zph() is alright. However, I guess that the plot y axis presents beta coefficient of s and it appears to vary during follow-up. The proportional hazards assumption states that the hazard of any variables must be constant throughout the study period. That is, hazard of s should not fluctuate (vary) with time. This plot shows that the hazard associated with s is less pronounced between 200 and 700 days. To me thats the graphical evidence for the p=0.000399 in the cox.zph().

Why did that happen? Subject matter will be your guide to decide why this occurred. I have not seen violations being as sudden as this one; the patterns are often more successive than your graph presents.

More importantly, you did the right thing to include the interaction term between s and stop. See John Fox example here.

Some would argue that you should be satisfied with that (without rechecking cox.zph(). I would recommend a recheck, however.

Adam Robinsson
  • 2,083
  • 3
  • 19
  • 39
  • 2
    Thanks Adam, I have actually solved this now. The violation is due to a handful of outliers (dirty data points) in the numeric `s` variable of a couple of observations. My takeaway lesson was `ALWAYS PLOT YOUR COVARIATES and CHECK FOR OUTLIERS` before fitting a Cox model. Cox regression is very prone to going haywire even by a couple of outliers. When I removed these, the `cox.zph` and the Schoenfield plots became normal. – Zhubarb Jan 04 '15 at 13:22