Consider the original formulation of the Lasso regression problem in a linear regression setting, as following$$
\min_\beta \|y - X \beta\|_2^2 \ \\s.t. \|\beta\|_1 \leq s
$$
To do the optimization, we utilize the Lagrange multiplier, and reformulate the problem as follows,
$$
\min_\beta \|y - X \beta\|_2^2 + \lambda \|\beta\|_1 \
$$
From the two formulations, you can see the connection between $\lambda$ and $s$.
(1) as $s$ becomes infinity, the problem becomes unconstrained problem, or ordinary least squares. Thus $\lambda$ becomes 0 accordingly;
(2) as $s$ becomes 0, all $\beta$'s shrink to 0, easily seen from first formulation. Therefore $\lambda$ would go to infinity.
That said, $\lambda$ and $s$ have reverse relationship. Now for your questions.
- How this constraining parameter $s$ is chosen?
In practice, you would just need to choose $\lambda$, mainly by cross-validation, as other people pointed out. You are not bothered by what the $s$ value would be.
- How are $\lambda, \, s$, and $\hat{\beta}$ shrinking to zero related to each other?
Have answered by Point (2) I made above.
- What is the decision process or how are some $\hat{\beta}$'s shrunk to zero and some are not?
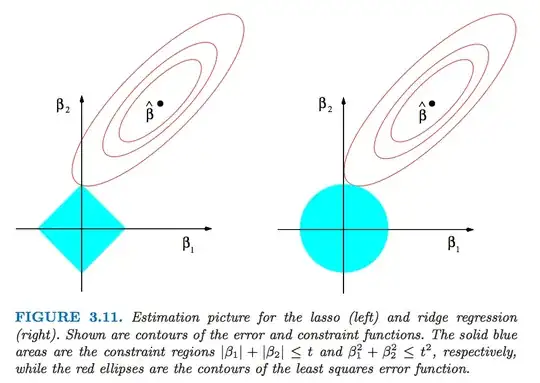
This has to do with the L1 constraint. I highly recommend the geometric representation of this problem at P71 of the book The element of statistical learning. The L1 constraint makes the feasible region to be a diamond (in terms of two $\beta$'s, as in the figure). The corners of the region would be "hit" by the function of the residual SS, resulting in shrinking some $\beta$'s to be 0. That's how the sparsity comes from.