I have a set of $N$ samples $s_{i}$, each one sampled from a normal distribution with standard deviations $\sigma_i$, which are known. I would like to know if the distributions have the same mean.
I think this situation is closely related to ANOVA, but the difference being that I only have one sample per 'group', and that I know the standard deviations of the group exactly.
As you describe them, your data constitute a mixture distribution. Assuming the distributions are known to be normal with known variances, the mean and variance of the mixture is:
\begin{align}
\mu_{\rm mixture} &= \sum_k p_k\mu_k \\
\sigma^2_{\rm mixture} &= \sum_k p_k\big((\mu_k - \mu_{\rm mixture})^2 + \sigma^2_k\big)
\end{align}
where $k$ indexes the component distributions and $p_k$ is the proportion of the mixture that each component constitutes.
Under your null hypothesis, the component mixtures all have the same means (for convenience, we can call it $0$). In addition, I gather the proportions are all $1/N$, since you have only one datum from each component. These facts simplify your situation quite a bit. Your data would have an expected variance equal to the sum of the known component variances. On the other hand, if the means vary then the variance of the component means can add considerably to the variance of your mixture.
Thus, you simply need to test if the variance of your data is greater than the sum of the known component variances. This can be done with a chi-squared test (see @Glen_b's anwer here: Why is the sampling distribution of a variance chi-squared?).
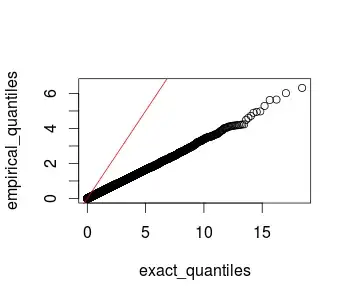
Here is a quick R demo: First I simulate the null hypothesis and show its distribution. Then I generate data where the null hypothesis is false and show the test. The data are three points drawn from normal distributions with means equal to $0$ (or they could have been anything else, so long as they are the same) and variances equal to $4$, $6$, and $8$. Thus the resulting mixture distribution variance is $18$. In this case there are three data points, so you have $2$ degrees of freedom.
set.seed(0884) # this makes the example reproducible
chi.vect = vector(length=10000) # this will store the test statistics
for(i in 1:10000){ # I do this 10k times
x = c(rnorm(1,0,sd=sqrt(4)), # here I generate the three data points
rnorm(1,0,sd=sqrt(6)),
rnorm(1,0,sd=sqrt(8)))
vx = var(x) # this computes the variance of the sample
chi.vect[i] = 2*vx / 18 # this computes the test statistic
}
x = c(rnorm(1, mean=30, sd=sqrt(4)), # these data come from distributions
rnorm(1, mean=20, sd=sqrt(6)), # w/ different means
rnorm(1, mean=10, sd=sqrt(8))) # x = 29.26698 26.00434 13.89382
vx = var(x) # vx = 65.60725
chi = 2*vx / 18 # chi = 7.289695
1-pchisq(chi, df=2) # p = 0.0261254
The qqplot gung has provided appears correct. But the plotted points do not closely follow y = x! This should be the case if the distribution was actually chi-squared. Here's a qqplot including the line y=x generated from the following code (adapted from gung's answer):
# Generates the q-q plot comparing the theoretical
# chi-squared distribution to the empirical distribution
# of the randomly sampled values:
empirical_quantiles = chi.vect[order(chi.vect)]
empirical_cdf = c(1:length(chi.vect))/length(chi.vect)
exact_quantiles = qchisq(empirical_cdf,df = 2)
plot(exact_quantiles,empirical_quantiles)
abline(0,1, col="red")
To answer the OP: Assuming $s_i \sim N(\mu, \sigma_i^2)$ and all $s_i$ are independent then you can do the following: \begin{equation} X_i := \frac{s_i}{\sigma_i}\\ \bar{X} := \frac{1}{n}\sum_{i=1}^n X_i \end{equation} Then it can be shown via Cochran's theorem that: \begin{equation} T := \sum_{i=1}^n (X_i - \bar{X})^2 \sim \chi^2_{n-1} \end{equation} So all you have to do is divide each $s_i$ by the known standard deviation, compute the mean and the the sum of squared deviations, and then compute a p-value from the chi-squared distribution with $n-1$ degrees of freedom. Note that a large value for $T$ corresponds to a large difference in mean so you want the upper tail of the chi-squared.
