0

note: A few people have marked this question as duplicate - But my question here is not answered in the other question. Though a fine distinction, what I was asking about here was not whether the signs of a factor matters in the absolute, but whether there was any significance to the relationship between factors (i.e. whether they were largely the same sign, or largely different signs).

So I am fairly familiar with factor analysis, and am aware of answers here and here that tangentially address my question. I believe I am right in my answer to the question I'm asking, but I wanted to make sure.

Essentially, I have, for each of several hundred participants, answers to two sets of almost identical questions. For examples' sake, let's say these are ratings of their current mood state on 10 items at the start (A) and the end (B) of a questionnaire survey. I expect that these mood rating items should load onto two main factors (positive and negative) and that these loadings should be consistent (i.e. both sets A and B should break down similarly into two factors).

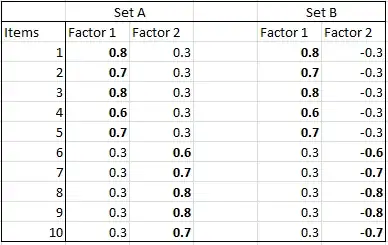
When I run the factor analysis, I find pretty much what I expected, except that for rating set A, items 1:5 load positively on factor 1, and items 6:10 load positively on factor 2, while for rating set B, items 1:5 load positively on factor 1, while items 6:10 load negatively on factor 2. Within each factor, the direction of the loadings are consistent across all items. This analysis was performed using varimax rotation.

Now, my understanding is that the difference between the two results is meaningless. Only the relative loading within each factor matters, and the reversal in sign is simply due to the factor analysis randomly converging on a factor that points in the opposite direction, but is essentially the same (except conceptually reversed). But I have had a colleague try to interpret the difference between the two analyses as meaning something with regards to the difference between the two factors.

Is my understanding right, or is there actually something to the difference?

A visual representation that might be more helpful - this is essentially what my output looks like:
Imgur

Community
  • 1
Sean Murphy
  • 591
  • 2
  • 8
  • 1
    The sign is arbitrary is you reverse it for the whole factor only. You can't change it for only part of the factor's loadings. You say `for rating set A... items 6:10 load positively on factor 2, while for rating set B... items 6:10 load negatively on factor 2`. Here one wants to ask - what's about loadings of items 1:5 with factor 2? If some of them are strong and are of the same sign in that factor in cases A and B, then factor 2 is considerably different in cases A and B. You perhaps might want to check 3-factor solutions then, to see if that's better. – ttnphns Oct 29 '14 at 07:52
  • I should clarify that the items I haven't specified as loading on a given factor have the same absolute loadings (.3 or less) across examples, and their direction relative to the items that do load does not alter either. Essentially, all loadings for all items are the same across sets A and B, except that the signs for the loadings on the second factor of set B are reversed. – Sean Murphy Oct 29 '14 at 07:57
  • 1
    (cont.) If however, those 1:5 loadings are small so you are going to neglect them (in interpretation of factor 2), then you can safely revert the sign of the factor and as it is virtually the same factor 2 as in case A. Btw, comparing two factor solutions by eye is not very reliable. Use procrustes rotation or confirmatory factor analysis for the comparison. – ttnphns Oct 29 '14 at 07:57
  • 1
    `all loadings for all items are the same across sets A and B, except that the signs for the loadings on thee second factor of set B are reversed` This sounds that factor 2 in case B is almost the same as in caase A, only completely sign-reversed. Then you are free to revert the sign "back"! – ttnphns Oct 29 '14 at 08:01
  • Thank you for taking the time to provide an answer! I will certianly look into CFA to compare the two solutions. So I am right in saying that there is nothing in set B itself (different to set A) that this sign reversal is attributable to, and that it is purely random in nature? – Sean Murphy Oct 29 '14 at 08:07
  • Sean, can you _show_ your loadings in your question, after all? It will help agains potential misunderstanding of you words, really. – ttnphns Oct 29 '14 at 08:07
  • I've added some example output that will hopefully clarify. – Sean Murphy Oct 29 '14 at 13:46
  • 1
    Following your added example: the two factor solutions are exactly the same. As I've said in the 1st comment, you may negate the sign of all the loadings of any factor. – ttnphns Oct 29 '14 at 15:31
  • Sean, in the thread your question is now marked as a duplicate of, it is explicitly discussed that the sign of PCA and FA scores can be reversed/flipped at will. So ttnphns's recommendation in the comment above: *"you may negate the sign of all the loadings of any factor"* (that you were happy to accept as an answer) -- is covered in that thread. How is that not a duplicate then? – amoeba Jan 19 '15 at 10:21
  • Amoeba - every example in the thread you linked refers to reversing the sign of both factors simultaneously. Saying that PCA scores can be reversed at will doesn't explicitly make clear whether this means you have to reverse the signs of all factors at once, or not, which was my question here. In fact, the diagrams in the other answer showing the factor rotation seem to indicate that you could not just flip the signs of 1 factor and not the other and maintain the same relationship, which is opposite this answer. I don't feel the information here is redundant - though others may differ. – Sean Murphy Jan 19 '15 at 21:11

0 Answers0