Draw a multinomial distribution from a Dirichlet distribution?

Question

I have a very rough understanding of the Dirichlet distribution and already seen some visualizations of its pdf over the 2-simplex, i.e., $\alpha$ is a 3D vector. However, I still do not understand the following statements that I have been frequently encountering with

Dirichlet distribution is a distribution over a multinomial distribution...

or

...draw a multinomial distribution from a Dirichlet distribution.

I would appreciate if someone could explain what these two statements mean, like to a non-statistian (a dummy).

Answer 1

Let's take a step back from the Dirichlet distribution and multinomial distribution and consider a slightly simpler set of models.

The binomial distribution describes the number of "successes" $y$ one expects to observe in a number of trials $n$. The binomial model has several key properties:

• The binomial model is dichotomous.
• Each event in a binomial model has a probability of "success" $\theta$.
• The trials in a binomial model are independent: previous successes neither increase nor decrease the probability of future successes.

This is all well and good when all of our data are subject to some kind of rigorous controls, so that we know that across all of our observations, the $\theta$ for each "batch" of trials is the same. But more realistically, we have reason to believe that $\theta$ for trial $y_i$ is different than for trial $y_j$. One way to accomplish this is to treat each $\theta$ as if it were drawn separately from a beta distribution. The beta distribution has several useful properties

• It is a probability distribution of probabilities: that is, it has support on the unit interval
• It is conjugate to the binomial model, which simplifies computations (I have intentionally omitted an extended discussion of conjugacy in this post and how that can simplify the process of drawing values from these distributions because I feel that is only tangentially related to your question.)

One method to draw values from a beta-binomial model is the following set of steps:

• Draw a value $\tilde{\theta}$ from the beta distribution.
• Draw a value $y$ from the binomial distribution with $\theta=\tilde{\theta}$.

This covers the simple case of a dichotomous, binary outcome. But you've asked about Dirichlet distributions. Happily, the Dirichlet distribution is actually the same thing as a beta distribution when the dimension is 2. In higher dimensions, it is analogous to the beta distribution.

Likewise, the multinomial distribution is the higher-dimensional analogue to the binomial distribution. In the case of a dichotomous outcome, the binomial distribution is the multinational outcome.

Drawing values from a multinomial distribution with a Dirichlet distribution over the probabilities of outcomes is accomplished in a very similar way:

• Draw a vector of probabilities from the Dirichlet distribution.
• Use that vector of probabilities to draw a vector of outcomes from the multinomial distribution.

Answer 2

I would appreciate if someone could explain what these two statements mean, like to a non-statistian (a dummy).

Let me try to do it by avoiding complex terminology.

First, you should understand what a simplex is. This answer explains it graphically: https://stats.stackexchange.com/a/296779/172825

To recap, every point in that simplex-triangle has a very nice property - it's in fact a particular multinomial distribution. Why? If you look at any point, its "vector" sums up to one and all "items" are between 0 and 1.

I tried to naively visualize Dirichlet distribution in the following figure.

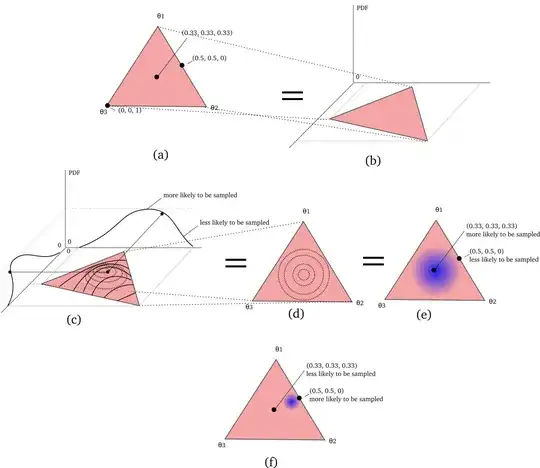
(a) shows a 3-simplex (as explained in the linked question). There are 3 example points shown with their "coordinates" so you can see that each of them is a multinomial distribution.

(b) let's put the triangle on the floor and the vertical axis be a probability density function

(c) is one particular example of Dirichlet distribution (I guess the parameters might be $\alpha = (2, 2, 2)$, roughly) - a kind of "mountain" in the middle of the triangle (sorry, I can't really sketch 3-D mountains easily). But you get the gist - the higher on that mountain, the higher the PDF value, thus the higher the chances a random sample will end-up here.

(d) just shows the "mountain" from the top as a contour-line plot; in reality the circles are not actual circles but that's a detail (e) is the same thing but using some kind of heat map (so the darker the blue is, the higher probability); such heat maps are shown in some literature on Dirichlet distribution

(f) is another Dirichlet distribution (different $\alpha$ parameters)

So what does it mean to "draw a multinomial distribution from a Dirichlet distribution"? You simply pick any point from that triangle (because every point is a multinomial distribution, remember?). Darker areas (or "higher" areas if you like the mountain analogy) just get higher chances to get sampled.

I'm not a statistician so I hope it's a correct explanation.