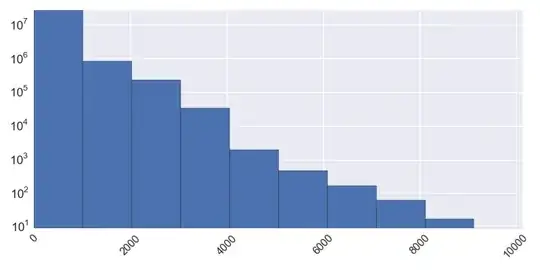
I have an empirical distribution that looks like the the image below and I hoping to model it with some parametric distribution. The X axis measures "number of buckets", while the Y axis measures **number of unique users in a given number of buckets*.
I am starting to explore the problem, but our prior knowledge about the problem would suggest that users choose to be in a bucket independently of each other and independently of other buckets they belong to.
For example the left-most bar in blue effectively shows that buckets of sizes between 0-1000 are the most common ones in the data.
From the list of "known" parametric distributions, what type of distribution could capture this problem or exhibit the pattern shown below?