8

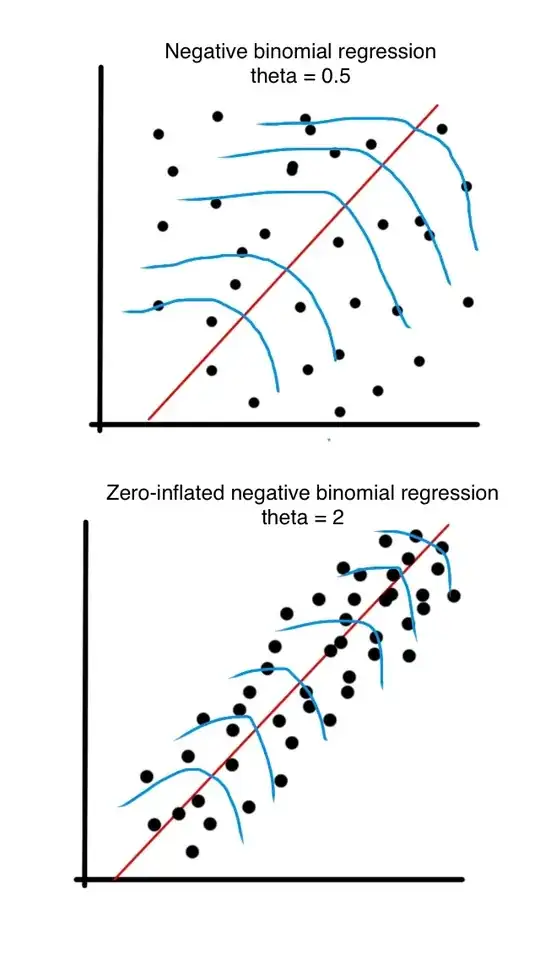
First off, a very similar question has been asked before. But the answers to this question did not explain what high/low values of theta mean. Here's my crack at trying to figure out what high/low values of theta mean. So please don't close this question!

Let's assume you've made two models: a negative binomial regression (NB) and a zero-inflated negative binomial regression (ZINB). The NB regression has a theta of 0.5 and the ZINB regression has a theta of 2. As I understand it, the higher theta in the ZINB regression indicates that more variance in the residuals has been accounted for, and therefore the negative binomial distribution that the model assumes has a more slender shape. Is this correct? Can anybody provide a more precise definition of the theta value, but without using equations?

I also quickly sketched a visualisation of my understanding. The residuals in the NB are more spread out, meaning the theta is smaller and the shape of the negative binomial distributions are more fat. The residuals in the ZINB are less spread out, meaning the theta is larger and the shape of the negative binomial distributions are more slender.

enter image description here

Community
  • 1
luciano
  • 12,197
  • 30
  • 87
  • 119
  • possible duplicate of [What is theta in a negative binomial regression fitted with R?](http://stats.stackexchange.com/questions/10419/what-is-theta-in-a-negative-binomial-regression-fitted-with-r) – Momo Sep 11 '14 at 09:35
  • 3
    I don't think it is useful to compare the theta of ZINB and a NB as they are different models. Apart from that, it really depends on the parametrization. In R's MASS, the relationship is the following: For a fixed $\mu$, the larger theta gets, the smaller the variance becomes. If theta is infinity, then the variance becomes $\mu$ (and then it is a Poisson). In other parametrizations (direct parametrization) a larger theta might mean larger variability. See Hilbes's post here http://stats.stackexchange.com/questions/10419/what-is-theta-in-a-negative-binomial-regression-fitted-with-r – Momo Sep 11 '14 at 09:35
  • Theta is parametrised the same in each model, at least in the `glm.nb` and `zeroinfl` functions in R. So theta is directly comparable in each model. Also, the question you link to doesn't provide an answer to my question—what is the interpretation of high/low theta values. – luciano Sep 11 '14 at 12:52
  • 3
    `zeroinfl` uses a finite mixture model with a negative binomial part and a point mass at zero. The former is similar to `glm.nb`, but the latter is not. Thus the theta in both models are not directly comparable as `glm.nb` will have a different theta than the `zeroinfl` model will have for the same data if there is positive mass on the excess zeros. That is simply because variability is different. For the interpretation of the high/low theta values, see the above comment again, for theta towards infinity the variance=mean. If theta towards 0 the variance>mean. – Momo Sep 11 '14 at 14:04

1 Answers1

7

$\theta$ is known as a dispersion parameter in GLM. But what does that really mean? Let me use an example to explain what the $\theta$ parameter is. Say you went to a party of mixed faculty members. You, as a statistician, looked for another statistician. Let $p$ be the probability of you succeeding in finding a statistician, and $X$ be the number of people you "randomly" approach and talk to, until you find the first statistician. $X$ follows a geometric distribution with the probability mass function:

$f(x) = P(X=x) = (1-p)^{x-1}p$

Now consider another example. You are interested in talking to 3 different statisticians. Then let us denote X as the number of people you "randomly" select until you find $r=3$ statisticians. $X$ now follows a negative binomial distribution with the probability mass function

$ f(x) = P(X=x) = \left( \begin{matrix} x-1\\ r-1 \end{matrix} \right) (1-p)^{x-r}p^r $

So the $\theta$ parameter, the $r$ in this probability mass function, represents the number of successful trials. When it is 1, $X$ follows a geometric distribution; otherwise, X follows a negative-binomial distribution.

So how does changing $\theta$ affects the shape of a distribution? With a give $p$, greater $\theta$'s result in greater spreads of $X$, hence the dispersion parameter. If you use R, you may want to get a feel by plugging in different values using dnbinom or rnbinom.

Masato Nakazawa
  • 1,702
  • 7
  • 9