3

I think I need to use a Poisson-family regression or negative binomial regression. My variables are as follows: Y is an integer value ranging from 0 to ~1200. It represents sums (number of species summed over an areal unit). There are in fact many zeroes but no negative values. X1 is a categorical variable, x2 is continuous (which also contains a few zeroes) and X3 is categorical. All are positive values. Variance of Y is larger than the mean. 

         Y            X1         x2                X3  
 Min.   :   0.00   01:29551  Min.   : 0.000   2009 : 2474  
 1st Qu.:   5.00   02:72289  1st Qu.: 7.646   2010:28484  
 Median :  23.00             Median :13.000   2011:  882  
 Mean   :  77.21             Mean   :12.634             
 3rd Qu.:  80.00             3rd Qu.:17.000             
 Max.   :1155.00             Max.   :30.000

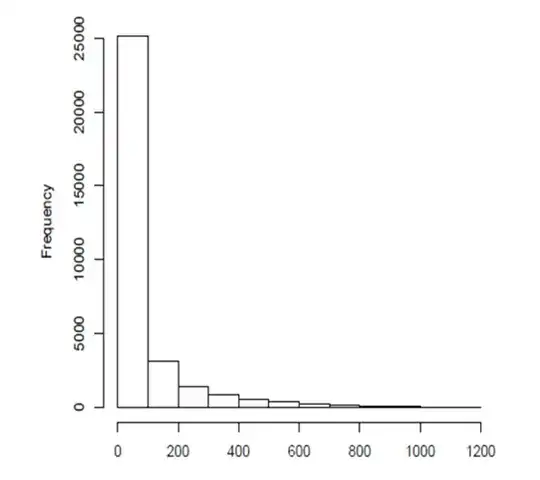
Histogram of Y

Y is negatively skewed (i.e., skewed to the left). Histograms of residuals from a basic linear model (lm) and a QQ plot indicates the results are also skewed. The residuals plotted against fitted values also indicate that a linear model may not be appropriate because more points are above the line than below (across all values of x). Is it correct to use GLM with a poisson distribution with log link in this case? 

Mydata.poisson  <- glm(Y~X1 +x2 + X3 +x2:X3, family=poisson, data=mydata)

Or more specifically, should I use the quasi-poisson? (in the regular poisson, my df was “31839 Total (i.e. Null); 31833 Residual”, Null Deviance was 1085000 and Residual deviance was 1079000). Also I believe this would be a case where I need to use a zero-inflated model? I am confused as to how to set this kind of model up. I read that a negative binomial distribution is similar to a poisson distribution, and better to use when the variance of your Y is greater than its mean, but isn't a binomial regression used when your response is binary?

EDIT: I have used the following negative binomial model: 

Mydata.nb  <- glm.nb(Y~X1 +x2 + X3 +x2:X3, data=mydata)

I understand that one should still check the residuals to see if the assumption of linearity holds (e.g., see discussion here: What are the assumptions of negative binomial regression?). A plot of the standardized residuals is included below and suggests that perhaps the relationship is not very linear. Would you agree? How can I resolve this?

Residual plot for Negative binomial model

Community
  • 1
sth
  • 265
  • 1
  • 4
  • 14
  • Your response is not binary, it's from 0 to 1200. – James Sep 02 '14 at 18:51
  • Yes that is exactly my point. I was wondering if there was a way to do negative binomial regression with a non-binary response. I guess not. – sth Sep 02 '14 at 19:26
  • Negative Binomial takes count data, just like Poisson. Binomial (logistic) takes {0, 1} response. – James Sep 02 '14 at 19:48
  • oh! You're right. I didn't understand that. Thank you. – sth Sep 02 '14 at 19:59
  • I'd like to see a plot of unstandardized residuals versus observed $y$ values, if it's at all readable. Also, what are you actually modeling here? Substantive understanding always helps. – shadowtalker Oct 08 '14 at 05:56

1 Answers1

1

  • I think the overdispersed Poisson won't work so well with this data, at least in the sense that it's not really going to deal with the high degree of skewness

  • The negative binomial model isn't linear (except with identity link, but the default in glm.nb is log link)

  • the linearity in question is in the linear predictor, which you can't so easily assess from the plot you have. There's some suggestion of changing variance (wider spread in the middle) which may also suggest a change in the mean, but it's hard to be sure if the mean changes from the plot, since it may just be the greater density of points. You might try scatter.smooth perhaps, to give a clearer indication.

You suggest you might need a zero-inflated model; that might indeed be a good thing to try, though it won't of itself fix that potential lack of fit that you think you might have.

Glen_b
  • 257,508
  • 32
  • 553
  • 939