I'm faced with a practical problem of solving for a 1-D function which has noise, so find myself in the territory of stochastic approximation (and I am well out of my comfort zone here!). I know there is some literature on the problem, but I've yet to find anything on the particular case I have in mind, where the noise is positive, to be precise: I can obtain values $f_i(x) = f(x)+\eta_i$ where the $\eta_i$ are noise, but also positive, and seek $x$ such that $f(x)=0$.
Thanks in advance!
[Edit, in response to comments]
I don't know for sure that the function $f$ is continuous, but it seems to be. Nor do I have any definitive information on the noise excepting its positivity (and I know that it is positive since the $f_i(x)$ are simulated annealing minimisations of a precisely defined objective); I do, however, have some empirical data -- here 1000 evaluations of $f_i(x)$ for a fixed $x$, the minimal value is 0.0588:
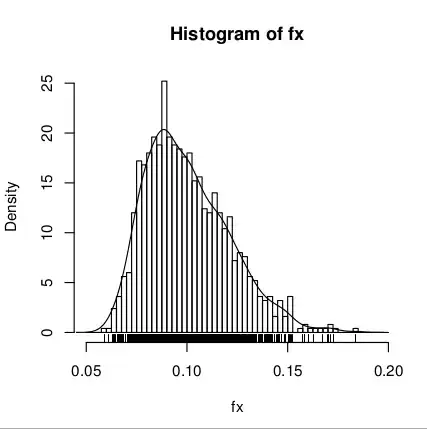
[Edit 2]
A "noisy plot" of the function $f(x)$ as requested in comments, there are multiple samples at some of the locations where the function is sampled, but not all. I am actually interested in $f(x) = 0.5$, so in terms of the original question, subtract 0.5 from $f$