0

I know this question has been asked in a slightly different form here. But my question differs and because of the forum rules I can't post on that thread. I have 2 independent variables, n=32, highly significant multiple regression, but only the intercept/constant has a significant p value.

Also, I've tested for multicollinearity, it's not in the readout from R below, but the variance inflation factor for the 2 dependent variables is 2.02. Durbin-Watson, added variable plot, P-P plot, standardized residuals plot, and cook's distance are all normal. Here's the R readout - please let me know what you think. 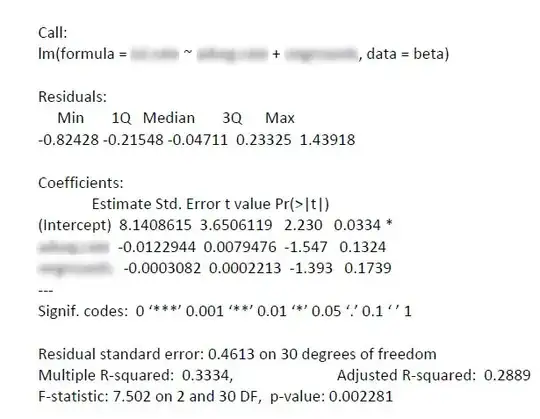enter image description here

SO: This topic is relevantly different since; what I'm searching for and still haven't found, is an actual explanation for what having a significant regression and no significant predictors means. How can this finding, if accurate, be explained? @Glen_b, I have seen that part of Jeromy's post (see my 2nd comment above) but how would I explain that in prose? Would it be accurate to say that the variables, together, have an effect on the outcome - but that their effects cannot be isolated from each other?

Community
  • 1
digits
  • 31
  • 5
  • 2
    Did you mean to say you have two *independent* variables? BTW, this looks like an *exact* duplicate. In order to keep the thread open, could you please be more specific about where you think the differences are? – whuber Aug 19 '14 at 20:43
  • 2
    It looks to me like several of the answers at your link directly address your question. Jeromy's answer, for example, says just what I'd say in response to your post if it wasn't a duplicate. Failing that being sufficient, look through some of the other posts under "Related" in the sidebar to the right -> – Glen_b Aug 19 '14 at 21:12
  • thanks, I do mean independent. And I did identify that the other thread has similarities. Relevant difference: The answers to that question DO NOT answer my specific question. Let's go point by point. first answer suggests too many variables included in that person's model tripped them up. I have two variables. second answer suggests multicollinearity and almost-significant predictors. tests show I have very low multicollinearity and my predictors are fairly far from p values of .05. But @Glen_B, if you think that makes the most sense, I'm inclined to reluctantly agree. Thank you – digits Aug 19 '14 at 21:33
  • I do not appreciate the downvotes.. Clearly, as anyone who read my post could learn, I was aware of the other literature, read through it, and was not satisfied of an answer. Furthermore, I couldn't even comment on that thread to ask another question. If this brand of censorship is the kind of reception users get on this website I will discontinue using it, and question whether this community fosters open inquiry or inhibits it – digits Aug 19 '14 at 21:37
  • 1
    Alex, I agree the downvotes are unwarranted, but I don't see any censorship going on. We are making an effort to connect you--and all future readers who find your question--to useful information without creating confusing redundancies on the site. ("Closing" redirects people to existing answers but does not delete the question or make it inaccessible.) As far as I and others can tell, some of the answers to the question you kindly researched and pointed out are applicable (two variables can easily be "too many") even though you have ruled out some of the other possibilities mentioned there. – whuber Aug 19 '14 at 21:52
  • 1) Two variables can be *too many* in the sense that it produces the effect in your question if the first variable and the second variable are reasonably correlated. Indeed they can even be fairly weakly correlated by the usual multicollinearity measures in the right situation. 2) The second part of Jeromy's answer points out a second mechanism you seem to have missed, so maybe you should take another look at it. It might be more help than you think. ... (ctd) – Glen_b Aug 19 '14 at 22:40
  • ... 3) there are *many* other posts in a similar vein here - dozens of them. I've answered different versions of this style of question several times already myself, and other people have produced better answers than mine on at least a couple more. If you don't sufficiently clearly explain how they fail to cover your situation, the correct behavior at this site is to close your question. That's not censorship, it's a deliberate design decision, to avoiding people answering the same question 100 more times half-heartedly every time it comes up when there are already many good, longer answers. – Glen_b Aug 19 '14 at 22:48
  • Fair enough, I understand there has to be a balance between openness and avoiding redundancy/halfhearted response. What I'm searching for and still haven't found, though, is an actual explanation for what having a significant regression and no significant predictors _means_. How can this finding, if accurate, be explained? @Glen_b, I have seen that part of Jeromy's post (see my 2nd comment above) but how would I explain that in prose? Would it be accurate to say that the variables, together, have an effect on the outcome - but that their effects cannot be isolated from each other? – digits Aug 20 '14 at 14:13
  • I still don't see any daylight between this Q & the duplicate. At the top you say "But my question differs", but that's it. I had thought about adding an answer here, but when I read Jeromy's post, there isn't anything of substance I would add. Re your questions in the comment, there is no deep meaning to be explained. You have 2 highly correlated predictors & very few data; you end up w/ a highly significant model & individual predictors that are close to significance, but not quite. If you had more data, you might have a clearer picture. – gung - Reinstate Monica Aug 20 '14 at 18:44
  • Okay - thank you for your patience. I think that with my novitiate's knowledge of stats I was expecting more of statistics than it can actually give (not that I am in any way critical of the discipline, that would be ridiculous). Now that I know it can't yield meaning in these circumstances my life is forever changed :). Thanks all, close the question if you wish. – digits Aug 20 '14 at 20:59

1 Answers1

1

One thing that likely is occuring with only 32 cases is that you have very low power. It might be that your predictors are signficant, but are not showing so because your power is too low to catch this. Of course it would seem that then the model itself would also suffer from this problem, but the power for the two calculations might be different (I don't know in honesty if the power in your F and T tests is very different).

Can you get more than 32 cases? That is actually a pretty small number to run a regression on, and if more data is available this is a good idea regardless. Failing that I would calculate your power and see how low it is. If it is signficantly below .8 it raises real doubts about the results.

user54285
  • 751
  • 4
  • 9
  • Thank you. I'm afraid that in terms of data, this is it. Also, I should mention that I'm constrained to the multiple linear regression and that my situation is such that I cannot perform any more diagnostics or run different tests, so I have to interpret what you see here. Many thanks as always. – digits Aug 19 '14 at 20:40