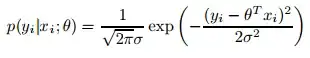Probabilistic interpretation of regression for justifying squared loss function

Question

I was reading Andrew Ng's CS229 lecture notes (page 12) about justifying squared loss risk as a means of estimating regressions parameters.

Andres explains that we first need to assume that the target function $y^{(i)}$ can be written as:

$$ y^{(i)} = \theta^Tx^{(i)} + \epsilon^{(i)}$$

where $e^{(i)}$ is the error term that captures unmodeled effects and random noise. Further assume that this noise is distributed as $\epsilon^{(i)} \sim \mathcal{N}(0, \sigma^2)$. Thus:

$$p(e^{(i)}) = \frac{1}{\sqrt{2\pi\sigma}}exp \left( \frac{-(e^{(i)})^2}{2\sigma^2} \right) $$

Thus we can see that the error term is a function of $y^{(i)}$, $x^{(i)}$ and $\theta$ as in:

$$e^{(i)} = f(y^{(i)}, x^{(i)}; \theta) = y^{(i)} - \theta^Tx^{(i)}$$

thus we can substitute to the above equation for $e^{(i)}$

$$p(y^{(i)} - \theta^Tx^{(i)}) = \frac{1}{\sqrt{2\pi\sigma}}exp \left( \frac{-(y^{(i)} - \theta^Tx^{(i)})^2}{2\sigma^2} \right)$$

Now we know that:

$p(e^{(i)}) = p(y^{(i)} - \theta^Tx^{(i)}) = p(f(y^{(i)}, x^{(i)}; \theta))$

Which is a function of the random variables $x^{(i)}$ and $y^{(i)}$ (and the non random variable $\theta$). Andrew then favors $x^{(i)}$ as being the conditioning variable and says:

$p(e^{(i)}) = p(y^{(i)} \mid x^{(i)})$

However, I can't seem to justify why we would favor expressing $p(e^{(i)})$ as $p(y^{(i)} \mid x^{(i)})$ and not the other way round $p(x^{(i)} \mid y^{(i)})$.

The problem I have his derivation is that with only the distribution for the error (which for me, seems to be symmetric wrt to x and y):

$$\frac{1}{\sqrt{2\pi\sigma}}exp \left( \frac{-(e^{(i)})^2}{2\sigma^2} \right)$$

I can't see why we would favor $p(e^{(i)})$ as $p(y^{(i)} \mid x^{(i)})$ and not the other way round $p(x^{(i)} \mid y^{(i)})$ (just because we are interested in y, is not enough for me as a justification because just because that is our quantity of interest, it does not mean that the equation should be the way we want it to, i.e. it doesn't mean that it should be $p(y^{(i)} \mid x^{(i)})$, at least that doesn't seem to be the case from a purely mathematical perspective for me).

Another way of expressing my problem is the following:

The Normal equation seems to be symmetrical in $x^{(i)}$ and $y^{(i)}$. Why favor $p(y^{(i)} \mid x^{(i)})$ and not $p(x^{(i)} \mid y^{(i)})$. Furthermore, if its a supervised learning situation, we would get both pairs $(x^{(i)}, y^{(i)})$, right? Its not like we get one first and then the other.

Basically, I am just trying to understand why $p(y^{(i)} \mid x^{(i)})$ is correct and why $p(x^{(i)} \mid y^{(i)})$ is not the correct substitution for $p(e^{(i)})$.

Answer 1

Overall, you're correct; $p(x|y)$ will be a normally-distributed function of the size of the error. However, in general, you will be using multiple exogenously fixed input variables $x$ to predict a single output variable $y$, so we're rarely interested in guessing $x$ directly based on what we know about $y$.

An example will be helpful here: Suppose you have a set of pictures of animals and you want to know the type of animal present in each picture. Your $x$ will be an image, and $y$ will be the type of animal in the image. $p(y|x)$ makes a lot of sense--we're trying to find probabilistically the correct class label for each image.

$p(x|y)$ is kind of odd. It's a probability of a single image, given that the image's label is a cat. If you had a 256 x 256 pixel image with 16-bit pixels, there are 2^(2^20) different images you could make, which is going to make any individual image's probability so tiny as to pretty much defy interpretation.

If we wanted to know $p(x|y)$, we'll use Bayes' Law to compute $p(x|y) = \frac{p(y|x)p(x)}{p(y)}$

On the other hand, $p(y|x)$ could be represented as a single-variable normal distribution representing our belief in $y$ given that you know $x$, which is the task that is usually more tractable, and thus we're usually more interested in solving.

Answer 2

The issue I was having is since $e^{(i)}$ is a r.v in terms of $x^{(i)}$ and $y^{(i)}$. i.e.

$$e^{(i)} = y^{(i)} - \theta^{T} x^{(i)}$$

Then if we have:

$$p_{e}(e^{(i)}) = \frac{1}{\sqrt{2\pi\sigma}}exp \left( \frac{-(y^{(i)} - \theta^Tx^{(i)})^2}{2\sigma^2} \right)$$

when should we favor $p(x^{(i)} \mid y^{(i)})$ vs $p(y^{(i)} \mid x^{(i)})$? (basically, it depends what we observe!)

Basically the answer ends up being simple. We are interested in modeling $p(y^{(i)} | x^{(i)})$ because we want to predict y given x. So mathematically, $p(x^{(i)} \mid y^{(i)})$ vs $p(x^{(i)} \mid y^{(i)})$ are extremely similar and related by $p_{e}(e^{(i)})$. However, they different in terms of what they have fixed fixed (i.e. what is observed or given). If x is given, then its fixed. So because we usually have x during our prediction phase, then we just use the form of the conditional distribution we need, i.e. we use:

$$p(y^{(i)} | x^{(i)})$$

because we are given $x^{(i)}$. We do know what $p(x^{(i)} \mid y^{(i)})$ distribution looks like but its not useful since we usually are not given the label y without knowing its corresponding x.

Answer 3

I think a very simple approach to understanding why $p(e^{(i)}) = p(y^{(i)}|x^{(i)})$ and not $p(x^{(i)}|y^{(i)})$, for the case you have shown, is that the units of error $e^{(i)}$ are same as the quantity $y^{(i)}$ and also the units of $\beta x^{(i)}$. Now, the normal equation is not really symmetric in $x^{(i)}, y^{(i)}$ because if $x^{(i)}$ is a vector of order $N$ and $y^{(i)}$ is a vector of order $M$ then in the equation presented above $e^{(i)}$ will be of order $M$ and not order $N$. For simple linear regression with variable $x^{(i)}$ of order $1$ and $y^{(i)}$ or order $1$, this is not directly evident. Furthermore, the $\sigma^2$ in the equation for a higher order case will be the covariance matrix $\Sigma$ which will of the order $M\times M$, so the symmetry will not be there anymore.

Answer 4

I also find Andrew Ng's notes confusing because there is a subtle point that isn't explained. What they say is that the noise $\epsilon$ has Gaussian distribution. This ends up being essential. If you look at the equation of a Gaussian:

$$ Gau(x,y,\theta) = \frac{1}{\sqrt{2 \pi} \sigma} exp\left( \frac{(y - \theta^T x)^2}{2 \sigma^2}\right)$$

its just a function of 3 variables. When you have a value for all of the variables (i.e. its inputs are "fixed") it outputs some value. However, how you "fix" a value in probability matters a lot. If you "fix" a variable due to conditioning then it means that you do an integral and re-normalization, but simply fixing because you are querying what the probability of a certain value is observed does not change the form of the equation while condition does. In other words, they have (assume $\theta$ is not a r.v. nor bayesian for simplicity):

$$ p(\epsilon) = p(y - \theta^Tx) = p(x,y;\theta) = p(x \mid y; \theta) = p(y \mid x; \theta) = \frac{1}{\sqrt{2 \pi} \sigma} exp\left( \frac{(y - \theta^T x)^2}{2 \sigma^2}\right) $$

i.e. they are all literally (and in analytic form) the same equations and return the same numbers. However, this only happens because things are Gaussian. If the noise were something else this would not happen. i.e. what happens for them is:

$$ g(x,y;\theta) = p(x,y;\theta) = \frac{ p(x,y;\theta)}{ \int_y p(x,y; \theta) dy } = \frac{p(x,y;\theta)}{\int_x p(x,y ; \theta) dx} $$

which is not generally true (I only know it true for Gaussian distributions).

For example, notice that the distribution for the noise $\epsilon$ is just a function of three variables (2 r.v./random and 1 not r.v./random) $x,y$ and $\theta$. Depending on what type of condition and values $x,y$ have you will get different values. For example consider the following counter example I cooked up:

this example just shows that conditioning does indeed change things quite a bit. In fact, conditioning tells you which table to choose $X \mid Y$ or $Y \mid X$ or simply the joint $X,Y$. The value $\theta$ could hypothetically choose a different set of tables (obviously not shown). So the main points are:

1. things work so nicely in Ng's example because things remain Gaussian because they started off Gaussian
2. The way you fix things matters a lot. Just wondering what the probability is that you observe $Y=y$ is not the same as conditioning on the event $Y=y$ happening and then asking something else. Fixing due to conditioning changes the table, just fixing due to a query fixes a value but to does not change the which table your looking at.

---

Appendix:

Some other points I thought would be interesting is that in the context of MLE we are usually searching for some good value of $\theta$. Thus, we want to get the $\theta$ we care most according to our objective. In this case since in practice usually we observe $x$ and then want to predict $y$ it makes sense to take $\theta$ that optimizes such a value i.e:

$$ \theta \in arg \max_{ \theta } P( \cap^N_{n} Y = y_n \mid X=x_n ; \theta) $$

this matters because as I showed in the previous table, optimizing $p(x,y;\theta)$ or $p(x \mid y ; \theta)$ might be tractable (or not) but they are probably don't result in the same $\theta$'s, since they might be optimizing different equations. So at Glen_b said in the question its because:

Because you're trying to predict y from x ?

seems obvious but it seems they might even result in different estimators if your not careful.

Answer 5

I don't think this has anything to do with what you are trying to predict, rather I'd go with something along these lines: We have: $$p(e^{(i)}) = \frac{1}{\sqrt{2\pi\sigma^2}} exp(-\frac{(e^{(i)})^2}{2\sigma^2})$$ which can be re-written as: $$p(e^{(i)}) = \frac{1}{\sqrt{2\pi\sigma^2}} exp(-\frac{(y^{(i)}-\theta^Tx^{(i)})^2}{2\sigma^2})$$ Now the expression on the right hand side in the above equation can be interpreted as representing a probability distribution of some sort of relationship between x and y. Now if we say that $\theta^Tx^{(i)}$ represents the mean of this probability distribution, then because the mean is a constant value $x^{(i)}$ must be constant, i.e. in other words $x^{(i)}$ is fixed. Hence, this expression then equals $p(y^{(i)} \vert x^{(i)})$.

Note that $p(y^{(i)},x^{(i)})$ would imply that both $y^{(i)}$ and $x^{(i)}$ are variable and so neither $y^{(i)}$ nor $\theta^Tx^{(i)}$ in that expression would have a constant value. So none of them could be the mean.

Also note that we can write down $p(x^{(i)} \vert y^{(i)})$ but for that we'll need to first re-write the expression $y^{(i)} - \theta^Tx^{(i)}$ in the form $x^{(i)} - \alpha y^{(i)}$ where $\alpha$ is some constant dependent on $\theta$. In that case, $p(x^{(i)} \vert y^{(i)}) \sim \mathcal{N}(\alpha,\sigma^2)$. This is because the normal distribution is given by: $$p(z)_{z \in \mathcal{N}(\mu, \sigma^2)}= \frac{1}{\sqrt{2\pi\sigma^2}}exp(-\frac{(z-\mu)^2}{2\sigma^2})$$

Answer 6

the property of Normal distribution is If a random variable X has a normal distribution N(θ, σ2) a new random variable aX + b has a normal distribution N(aθ + b, a2σ2)

the response yi is a linear function of a set of features x:

y ( i ) = θ T x ( i ) + ϵ ( i )

Now, let us assume that all errors has a Normal Distribution N(0, σ2) Therefore, we can immediately know that yi will also follow a Normal Distribution N(θTx, σ2) by using the property we introduced at the beginning of the section: