Can anyone explain why having too many p-value less than 0.001 is alarming? Like what happens to my model right now:
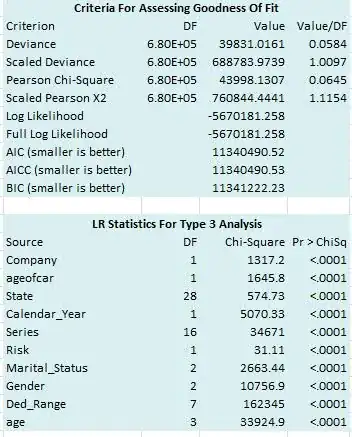
All independent variables are categorical except for Calendar_Year. There are 682211 observations in my data set.
Can anyone explain why having too many p-value less than 0.001 is alarming? Like what happens to my model right now:


All independent variables are categorical except for Calendar_Year. There are 682211 observations in my data set.
Remember that p-values are a function of the t/Wald/whatever statistic you're using, which in turn is usually a function of standard error of the estimate and the size of the estimate. And standard error is often a function of sample size.
So two things can cause "too many" very small p-values:
The first case is obvious: if the magnitude of your estimate is biased upward, then you think it's larger than it is, so you might erroneously reject a null hypothesis that it is, in fact, zero.
In the second case, standard error is something like an estimate of the uncertainty surrounding your parameter estimate. If you estimate that uncertainty to be too small, you might, again, erroneously reject a null hypothesis of zero for the parameter in question.
What constitutes "too many" is not only situation-specific but also subjective, once you've checked for sources of bias (e.g. heteroskedasticity can bias your standard errors). I don't know what your units of measurement are, but the only thing left to do here is ask yourself "Does a coefficient of -0.0550 on FUSION 4D 2WD make sense? Is it big enough to be meaningful?"
From the comments, with regard to the effect of sample size in particular:
Sample size doesn't distort the estimate, but standard error is a function of sample size. I don't use the word "distort" because this is by design -- the larger your sample, the more precise your estimate. But this "estimate of the precision of your estimate" is not robust to other problems that are not cured by sample size. If those problems are not accounted for, you can be falsely emboldened by your very small p-values.
Also, remember that "statistical significance" does not imply substantive significance. All it says is that "given the amount of noise in the data, this coefficient is distinguishable from zero." But it's incredibly unlikely that the coefficient is ever exactly zero, so in very large samples you will pick up on increasingly meaningless deviations from zero as "statistically significant." The ironic dark side of asymptotic frequentist statistics is that the underlying model of "true" fixed coefficients is complete bunk... yet this is only an issue in very large samples.
And the example due to user Penguin_Knight:
Not "distorted" per se, just that they go down when your sample size goes up; it's just the nature of these tests. Let's say in a town the men are 0.0001 cm taller than the women on average. With a sample size of 150 you may not detect that, with a sample size of 150,000 you may. The mean difference does not change, but just by enrolling more people the SE will go down, and so will the p-value. So, you should recast another look at the difference 0.0001 cm, is it an important difference? This question, statistics cannot answer for you.