$\newcommand{\E}{\mathbb{E}}$(I'm writing this assuming you're familiar with manipulating probability distributions and expectations, but hopefully nothing too fancy. Let me know if I should explain anything more. I'm also doing this in a fairly computational way to just get an answer rather than attempting to do it all out by hand.)
Say we have $n = 5$ players each rolling up one characters with 6 ability scores, each denoted as $X_{ij}$. Define $Y_i = \sum_{j=1}^6 X_{ij}$ to be the sum of the $i$th player's ability scores. Then you're asking about the expectation of $Z = \max_{i, i'} \lvert Y_i - Y_{i'} \rvert = Y_{(n)} - Y_{(1)}$, using the notation that $Y_{(1)}$ is the first sorted value from $\{Y_1, \dots, Y_n\}$ (i.e. the minimum), and $Y_{(n)}$ is the $n$th (the maximum).
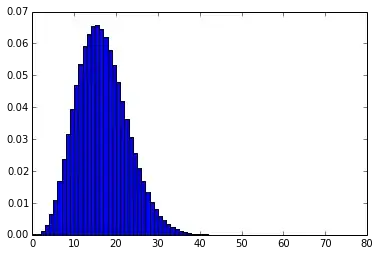
Individual scores $X_{ij}$
The easiest way to find the distribution of $X_{ij}$, as in the answer you linked, is to just brute-force it by considering all $6^4 = 1296$ possible rolls. Here's some quick Python code (there's probably a better way to do this...):
import numpy as np
import matplotlib.pyplot as plt
def as_kth_of(a, k, n):
'''vector a => shape (1, ..., 1, a.size, 1, ..., 1)
where new shape is length n, a.size is in kth'''
return a[(np.newaxis,) * k + (slice(None),) + (np.newaxis,) * (n - k - 1)]
def pmf_drop_lowest(sides, number):
rolls = np.arange(1, sides + 1)
totals = sum(as_kth_of(rolls, k, number) for k in xrange(number))
mins = np.ones_like(totals) * 10000
for k in xrange(number):
mins = np.minimum(mins, as_kth_of(rolls, k, number))
return np.bincount((totals - mins).ravel()) / totals.size
score_pmf = pmf_drop_lowest(6, 4)
plt.bar(np.arange(score_pmf.size) - .5, score_pmf)
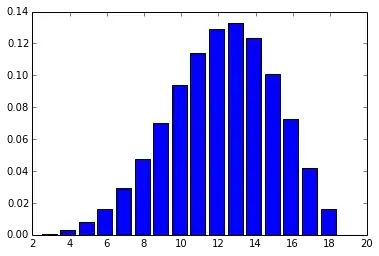
Total ability score $Y_i$
Now we can find the distribution of the sum of ability scores, $Y_i = X_{i1} + X_{i2} + \dots + X_{i6}$.
What's the distribution of the sum of two independent, discrete random variables $A + B$?
Well, $\Pr(A + B = c) = \sum_{k=-\infty}^\infty \Pr(A = k) \Pr(B = k - c)$. It turns out that this operation is known as convolution, and luckily numpy has a function to do it for us. (The linked Wikipedia article doesn't have much about it for probability; you could try this chapter of Grinstead and Snell.)
Code:
total_pmf = 1
for _ in xrange(6):
total_pmf = np.convolve(total_pmf, score_pmf)
plt.bar(np.arange(total_pmf.size) - .5, total_pmf)
Highest and lowest values of $Y$
Now that we know the distribution for $Y_i$, our question is: what is the max pairwise distance between two elements of $Y$? Alternatively, what is the difference between the highest and the lowest $Y$?
Writing the variable we care about as $Z = Y_{(n)} - Y_{(1)}$,
we have that $\E Z = \E Y_{(n)} - \E Y_{(1)}$,
since expectation is linear.
This saves the work that I did in originally writing up this answer in computing the joint distribution of the two. :)
First, let's define the cumulative distribution function (cdf) $\Pr(Y \le y) = \sum_{k=0}^y \Pr(Y = k)$.
Then, the cdf of $Y_{(n)}$ is
$$\begin{align*}
\Pr(Y_{(n)} \le y)
&= \Pr\left( Y_1 \le y \text{ and } Y_2 \le y \text { and } \dots \text { and } Y_n \le y \right)
\\&= \prod_{i=1}^n \Pr\left( Y_i \le y \right)
\\&= \Pr(Y \le y)^n
\end{align*}$$
since the $Y_i$ are independent.
Then, because $Y_{(n)}$ takes nonnegative integer values,
we can compute its expectation as
$$\begin{align*}
\E Y_{(n)}
&= \sum_{y=1}^\infty \Pr(Y_{(n)} \ge y)
= \sum_{y'=0}^\infty \Pr(Y_{(n)} > y')
\\&= \sum_{y'=0}^\infty \left( 1 - \Pr(Y_{(n)} \le y') \right)
= \sum_{y'=0}^\infty \left( 1 - \Pr(Y \le y')^n \right)
.\end{align*}$$
Code:
n_players = 5
total_cdf = np.cumsum(total_pmf)
exp_max = np.sum(1 - total_cdf ** n_players)
getting exp_max about 81.5.
Similarly, for the min:
$$\begin{align*}
\Pr\left( Y_{(1)} \le y \right)
&= 1 - \Pr\left( Y_{(1)} > y \right)
\\&= 1 - \Pr\left( Y_1 > y \text{ and } \dots \text{ and } Y_n > y \right)
\\&= 1 - \Pr\left( Y_i > y \right)^n
\\&= 1 - \left( 1 - \Pr\left( Y \le y \right) \right)^{n}
\end{align*}$$
and its expectation is:
$$
\E Y_{(1)}
= \sum_{y=0}^\infty \Pr(Y_{(1)} > y)
= \sum_{y=0}^\infty \left( 1 - \Pr\left( Y \le y \right) \right)^n
$$
Code:
exp_min = np.sum((1 - total_cdf) ** n_players)
getting exp_min about 65.3.
The final expected difference between the luckiest and unluckiest of 5 players is then a total of 16.2 ability points. (That's kind of a lot!)
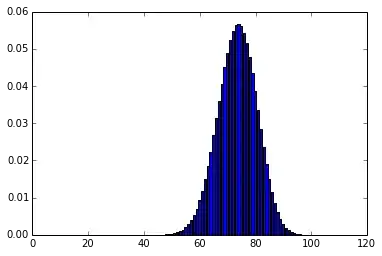
By the way, I mentioned that I computed the joint distribution of $Y_{(1)}$ and $Y_{(n)}$ (as $\Pr(Y_{n} = y') \Pr(Y_{(1)} = y \mid Y_{(n)} = y')$). It turns out that for five players, the distribution of $Y_{(n)} - Y_{(1)}$ looks like this: