I would like to know if it is possible to convert a normal distribution into a triangular distribution. If it is, how it can be done?
I know the mean and the coefficient of variation of the normal distribution.
I would like to know if it is possible to convert a normal distribution into a triangular distribution. If it is, how it can be done?
I know the mean and the coefficient of variation of the normal distribution.
Yes, it is possible. Basically, what you need is a function $T:{\mathbb R}\rightarrow[a,b]$ such that $F_{a,b}(x)=\Phi_{\mu,\sigma}\left[T\left(x\right)\right]$, where $F_{a,b}$ is the triangular distribution on $[a,b]$, $\Phi_{\mu,\sigma}$ is the normal distribution with mean $\mu$ and variance $\sigma^2$, and $x\in[a,b]$. Then,
$$T\left(x\right)=\Phi^{-1}_{\mu,\sigma}[F_{a,b}(x)].$$
For $\mu=0,\sigma=1,a=-1,b=-1$, $T$ looks as follows
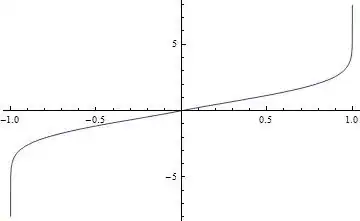
Also, note that the argument used by @COOLSerdash is valid, but the uniform is on the closed interval $[0,1]$, otherwise you cannot transform it into a closed interval $[a,b]$.