1

I am confused about how to apply a transformation to my predictor/response variables to test curvilinear relationships. I read about log transformations, polynomials, quadratic functions. But I am not a statistician. How do I choose which to apply in my regression formula?

My hypothesis relevant in my industry (advertising) is : (i) at low volume of predictor, the impact on my response variable exists but is limited. There's not enough critical mass of predictor. (ii) at optimal volume, the impact on my response variable is increasing at an increasing rate. (iii) Beyond a point, the predictor's impact on response variable becomes limited.

vagabond
  • 375
  • 1
  • 2
  • 14
  • 1
    Unless there is reasoning based on findings in your field, usually the analyst can only guess what relationships may exist. However, **plotting the data** can be extremely useful here. You can control for other variables by running a regression without your non-linear transformation and plot the residuals from these models against the non-linear transformation to see if you get a strong trend. –  Jul 25 '14 at 18:33
  • Thanks Matthew, Are you suggesting that I plot the residuals from regression with non-linear transformations against residuals from regression without any transformations? If yes, how do I analyze the plot? – vagabond Jul 25 '14 at 18:40
  • Not quite. Say you have some other predictors (possibly including a linear version of your variable) and you want to evaluate a non-linear transformation of a particular variable. Run a regression on all the parameters without that non-linear transform, and then plot the residuals of that model against the nonlinear transformation. [Here](http://i.imgur.com/PRCqag3.png)'s an example of what I mean. The y-axis are the residuals from a model without $\log(X_3)$ and the x-axis is the actual variable $\log(X_3)$. This can help you see if there exists a trend while controlling for other variables. –  Jul 25 '14 at 18:46
  • 1
    However, it is worth noting that that is NOT a statistically valid model selection procedure... purely an exploratory tool. –  Jul 25 '14 at 18:46
  • @matthew so I can check whether some portion of the residuals can be accounted for by the transformed variable or not. I just saw the example. The plot tells us that at higher values of log(x3) the residual value keep increasing. Basically there is a relationship between the two and hence the log transformation could be a useful addition to the regression. Am I getting it? – vagabond Jul 25 '14 at 18:51
  • I'm going to submit an answer with a better explanation –  Jul 25 '14 at 18:56
  • 1
    An illustrated worked example of one possible method to identify effective nonlinear re-expressions of regression variables is provided at http://stats.stackexchange.com/a/35717. – whuber Jul 25 '14 at 22:30

1 Answers1

3

Going to preface my answer with this: the procedure I describe below is NOT a valid model selection procedure... It is an exploratory tool.

How do I choose which to apply in my regression formula?

Unless there is reasoning based on findings in your field, usually the analyst can only guess what relationships may exist. One way to do this is to throw all sorts of non-linear transformations into the regression model to see how well they do in explaining the output variable.

However, plotting the data can be extremely useful here. Consider a model given precisely by $$ Y \sim \mathcal{N}(\mu, \sigma^2),\\ \mu = \beta_0 + \beta_1X_1 + \beta_2 X_2 + \beta_3\log(X_3). $$ If we suspect there is a nonlinear transform for $X_3$ that will help us model $Y$, then we can run a regression on $Y$ against just $X_1, X_2$ and look at the residuals. The residuals are the errors of the model (i.e., $y - \hat y$), so they represent how far off just using $X_1, X_2$ is. In this case, we would expect $y - \hat y \propto \log(X_3)$ because of the formula for $\mu$: $$ \mu = \beta_0 + \beta_1X_1 + \beta_2 X_2 + \beta_3\log(X_3) \implies \mu - (\beta_0 + \beta_1X_1 + \beta_2 X_2) = \beta_3\log(X_3) $$ Plotting the residuals, we observe a log trend in $X_3$.

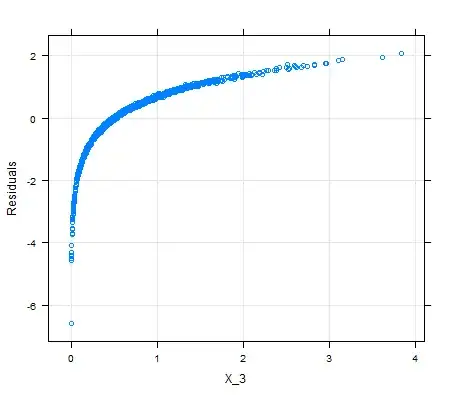
enter image description here

So we plot $\log(X_3)$ against the residuals and get a clearly linear trend.

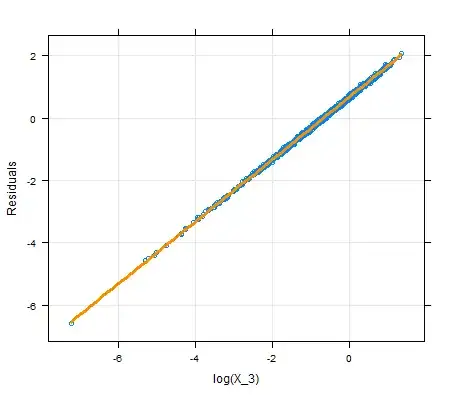
enter image description here

Just plotting $X_3$ against $Y$ might not be that useful, since we wouldn't necessarily be able to uncover this trend without controlling for $X_1, X_2$. This approach allows you a better chance to uncover $X_3$'s involvement in predicting $Y$.

  • well, I don't know what to do. After trying log transformations, 2nd & 3rd degree polynomials and quadratic functions, I find the simple non-transformed values explain the relationship best. Except now I have two highly collinear variables interacting with each other and I need both of them since I want to compare them relatively. – vagabond Jul 25 '14 at 20:26