Graphical comparison of regression models

Question

Will a graph on predicted and measured values plotted for two models separately be helpful in comparing them?

Answer 1

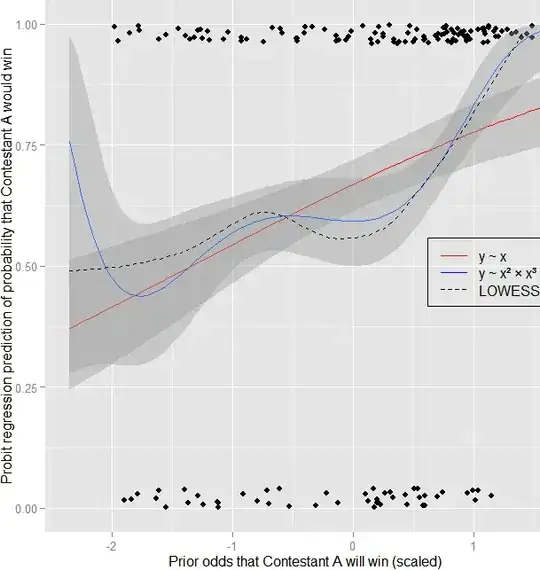
Yes, by all means, visualize your data whenever there's the slightest excuse. I even do it when I'm asked not to! Here's an example from a hobby analysis of mine using logistic regression. Compare:

glm(y~scale(x),family=binomial(link=probit))                   #First-order model vs. 
glm(y~I(scale(x)^2)*I(scale(x)^3),family=binomial(link=probit) #Interacting polynomial model
                                                               #Plotting code in R follows:
require(ggplot2);ggplot(mmath,aes(x=scale(TapologyOddsSharkAOdds),y=AWinBLose))+ 
geom_point(position=position_jitter(width=0,height=.04))+geom_smooth(lty=2,col='black',se=F
)+stat_smooth(method=glm,family=binomial(link=probit),col='red')+
stat_smooth(formula=y~I(x^2)*I(x^3),method=glm,family=binomial(link=probit))+
scale_y_continuous('Probit regression prediction of probability that Contestant A would win'
,lim=0:1)+scale_x_continuous('Prior odds that Contestant A will win (scaled)')

Forgive the busy chart, but I think this tells the comparative story best so far. It's a probit regression model of contest outcomes based on odds estimated by expert judges. The red one is the simple model, the blue one is a wacky interacting polynomial model, and the dotted black line is a LOWESS line, which I generally like to add to my plots to see what something sort of nonlinear and overfitted would look like. I don't take the LOWESS model very seriously otherwise, largely because I honestly don't understand it, but also because its bumps are basically atheoretical and exploratory.

The simple linear model makes sense, and works reasonably well. Its AIC = 382.28.

Coefficients:          Estimate Std. Error z value Pr(>|z|)    
(Intercept)             -0.3690     0.1932  -1.910   0.0562 .  
x                        1.3284     0.3023   4.394 1.11e-05 ***
Null deviance: 397.73 on 310 degrees of freedom; Residual deviance: 378.28 on 309 df

The polynomial model doesn't make as much sense, but seems to fit even better..? Its AIC = 374.48.

Coefficients: Estimate Std. Error z value Pr(>|z|)    
(Intercept)    0.23423    0.11937   1.962  0.04974 *  
I(x^2)         0.33684    0.13540   2.488  0.01286 *  
I(x^3)         0.45981    0.09743   4.719 2.37e-06 ***
I(x^2):I(x^3) -0.06350    0.02291  -2.772  0.00557 ** 
Null deviance: 397.73 on 310 degrees of freedom; Residual deviance: 366.48 on 307 df

However, there are a number of reasons not to trust the polynomial model. Most of them are tangential (not sure if it's OK to exclude the first-order term, hard to justify all the wiggles theoretically, purely exploratory, etc.), but one particular problem I'm not comfortable with is that big upward jump at the far left end. A prior odds estimate of x=.99 could be reexpressed as x=.01 if I swap my designations of "Contestant A" and "Contestant B", which are assigned arbitrarily. In my dataset, max(x)= .99, but max(y) = .03. An x=.01 corresponds to a $Z(x)=-2.36$, which is in the danger zone of inflated predictions and probably a very large residual, because that contestant would almost certainly lose (y = 0) – note that y = 1 (indicating victory) invariably for $Z(x)\ge1.25$.

The punchline: I wouldn't have realized that the model has that big, inappropriate upturn for extremely low odds if I hadn't plotted it. It might be making better predictions for me so far, as it does follow the LOWESS line much better and seems to recognize the near-certainty of victory when x is very high...but if I ever get a very low x outside the training sample, I can expect a silly prediction, which is good to know in advance. Furthermore, this is evidence that I need to ask some questions of my own regarding this polynomial model and how I'm assigning Contestant A status...In any case I ♥ ggplot!