3

This may be a silly question, but I can't find a concise answer. I've been studying Convergence of Random Variables in Wasserman's All of Statistics, which starts out by explaining:

$X_n$ is a sequence of random variables: $\{X_1, X_2, ... X_n\}.$

It then goes on to define the law of large numbers:

$\bar{X_n} = n^{-1} \sum_{i=1}^{n} X_i$ converges in probability to $\mu = \mathbb{E}(X_i)$

This seems like a mean to me, however I'm struggling to understand this intuitively. Am I supposed to be visualizing the addition of random number distributions, which could eventually end as a point-mass at the expected value? But couldn't $\mathbb{E}(X_i)$ resolve to many possible numbers since the relatedness of the sequences of $X$s is unknown?

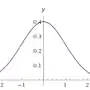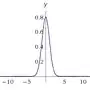enter image description here + enter image description here = enter image description here?

Or am I taking just a sample from each distribution to add?

$\bar{X_n} = n^{-1} \sum_{i=1}^{n} \{x$ $\epsilon$ $X_i\}$?

My problem is that the concept of adding random variables (as opposed to samples from them) was never defined. I'm assuming I just add the closed form representation of their distributions, but you know what they say about assumptions...

Thanks!

lucidv01d
  • 133
  • 2
  • The addition of random variables is described in our thread at http://stats.stackexchange.com/questions/95993/can-anyone-clarify-the-concept-of-a-sum-of-random-variables. Does this answer your question? – whuber Jul 22 '14 at 13:56

2 Answers2

2

By the way the LLN is described in your case, the assumption is that all $X_i$ have the same expected value (you have $Ε(Χ_i) = \mu \;\;\forall i$). So, no, $E(X_i)$ cannot resolve to many different values, it is the fixed $\mu$.

Then the statement is that the sample average converges to the common expected value.

This generalizes: for random variables with different expected values, we have

$$\frac 1n \sum_{i=1}^nX_i \xrightarrow{p} \frac 1n \sum_{i=1}^nE(X_i)$$

Needed conditions differ, you should look them up.

And, no, you do not add "samples" (i.e. realizations) of the random variables, you consider the sum of the random variables themselves (which are real-valued functions). And this is the whole "point" of the law: the average sum of functions converges in probability to the average sum of numbers.

Alecos Papadopoulos
  • 52,923
  • 5
  • 131
  • 241
0

Good question. Actually, there are many laws of large numbers, so the definite article is a misnomer. However, all of them say essentially the same thing: A sequence of means converges to a constant, representing the mean of the system. The various LLNs differ in their assumptions about the properties of the sequence of random variables and in the mode of convergence.

Under the setup Wasserman is giving, you can think of the sequence of random variables as being a simple random sample of increasing size from an infinitely large population. Convergence appears to be in probability, resulting in one version of the Weak Law of Large Numbers. Proof of convergence is via Chebyshev's inequality.

Dennis
  • 1,710
  • 9
  • 15