How to decide which penalty measure to use ? any general guidelines or thumb rules out of textbook

Question

A number of regularization measures are available in literatures, which is kind of confusing to beginners. The classical penalty is ridge by Hoerl & Kennard (1970,Technometrics 12, 55–67).

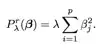
Another modification to this is lasso by Tibshirani (1996, Journal of the Royal Statis- tical Society B 58, 267–288), defined as:

Another penalty is the elastic net penalty (Zou and Hastie 2005, Journal of the Royal Statistical Society B 67, 301–320) , which is a linear combination of the lasso penalty and the ridge penalty. Therefore the penalty covers these both as extreme cases.

The another penalty that I could find is bridge penalty introduced in Frank & Friedman (1993, Technometrics 35, 109–148). where λ ̃ = (λ, γ). It features an additional tuning parameter γ that controls the degree of preference for the estimated coefficient vector to align with the original, hence standardized, data axis direc- tions in the regressor space. It comprises the lasso penalty (γ = 1) and the ridge penalty (γ = 2) as special cases.

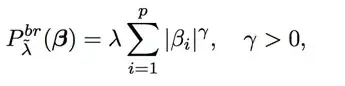
My question is : are there any preferences on type of penalty to use - something from or out of statistical text books ? Or this is just trial and error ? Please explain to layman language.

Answer 1

There can be many considerations to this matter. To name a few:

1. Inference: the distribution of ridge estimates is fairly simple to derive. Lasso, and basically any other penalty that performs variable selection, has only limited probabilistic results.
2. Sparsity: If you desire a model with only a few predictors (say, for speed of prediction, for interpretability, ...) then you will want $l_1$ regularization.
3. Speed of computation: The time complexity of the learning can be a consideration. There are differences between the algorithms. See here for some guidance. This becomes especially important if you plug the whole procedure in a cross validation scheme where models are fitted repeatedly.