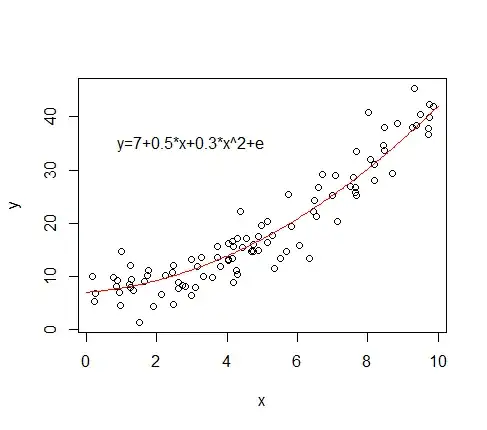
If I have the below functional form for an OLS regression, how do I interpret the $x$ and $x^2$? I cannot interpret them separately, correct? Do I interpret them as a summation of the two coefficients, so the effect of a one unit change of $x$ on $y$ is $0.5 + 0.3 = 0.8$?
$$ y = a + 0.5x + 0.3x^2 + e $$
Update: Now with 2 squared terms, and one that is an interaction term with the other and a binary variable, is there no rule for how to interpret the coefficients for all values of $x$? Or does it depend on the value of $x$?
\begin{align}
y = 0.04\; &+\; 0.05\times {\rm drop}\; +\; 0.008\times {\rm season}\; -\; 0.0004\times {\rm season}^2 \\
&+\; 0.002\times {\rm dropseason}\; -\; 0.0003\times {\rm dropseason}^2\; -\; 0.029\times p \\
&-\; 0.01\times r_1\; +\; 0.003\times r_2\; +\; 0.01\times r_3\; +\; 0.003\times v_5\; +\; e
\end{align}