13

What is the importance of hat matrix, $H=X(X^{\prime}X )^{-1}X^{\prime}$, in regression analysis?

Is it only for easier calculation?

amoeba
  • 93,463
  • 28
  • 275
  • 317
user 31466
  • 1,197
  • 13
  • 31

3 Answers3

18

In the study of linear regression, the basic starting point is the data generating process $ \textbf{y= XB + u} \quad $ where $ \textbf{u} \sim N(0,\sigma^2 \boldsymbol I) $ and $\textbf{X}$ deterministic. After minimizing the least squares criterion, one finds an estimator $ \widehat {\textbf{B} }$ for $\textbf{B}$, i. e. $ \widehat {\textbf{B}}= ( \textbf{X} ' \textbf{X})^{-1}\textbf{X} '\textbf{y}$. After plugging in the estimator in the initial formula, one gets $\widehat {\textbf{y}}=\textbf{X}\widehat {\textbf{B}}$ as a linear model of the data generating process. Now, one can substitute the estimator for $\widehat {\textbf{B}}$ and gets $\widehat {\textbf{y}}=\textbf{X}( \textbf{X} ' \textbf{X})^{-1}\textbf{X} '\textbf{y}.$

So, $\textbf{H} = \textbf{X}( \textbf{X} ' \textbf{X})^{-1}\textbf{X} '$ is actually a projection matrix. Imagine you take all variables in $\textbf{X}$. The variables are vectors and span a space. Hence, if you multiply $\textbf{H}$ by $\textbf{y}$, you project your observed values in $\textbf{y}$ onto the space that is spanned by the variables in $\textbf{X}$. It gives one the estimates for $\textbf{y}$ and that is the reason why it is called hat matrix and why it has such an importance. After all, linear regression is nothing more than a projection and with the projection matrix we cannot only calculate the estimates for $\textbf{y}$ but also for $\textbf{u}$ and can for example check whether it is really normally distributed.

I found this nice picture on the internet and it visualizes this projection. Please note, $\beta$ is used instead of $\textbf{B}$. Moreover, the picture emphasizes the vector of the error terms is orthogonal to the projection and hence not correlated with the estimates for $\textbf{y}$

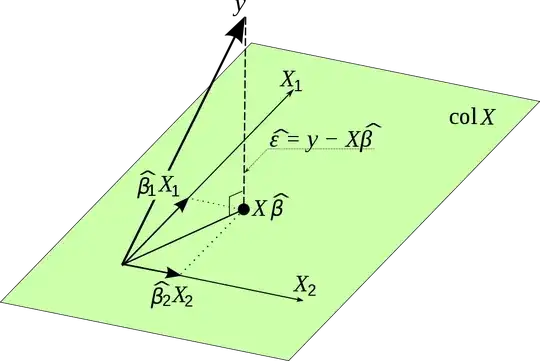
enter image description here

random_guy
  • 2,262
  • 1
  • 18
  • 30
6

The hat matrix is very useful for a few reasons:

  1. Instead of having $\widehat{y}=Z\widehat{\beta}$, we get that $\widehat{y}=Py$ where $P$ is the hat matrix. This gives us that $\widehat{y}$ is a linear mapping of the observed values.
  2. From the hat matrix $P$, it is easy to calculate the residuals $\widehat{\epsilon}$. We see that $\widehat{\epsilon}=y-\widehat{y}=y-Py=\left(I_n-P\right)y$.
wilsnunn
  • 161
  • 5
0

It's nothing more than finding the "closest" solution for Ax = b where b is not in the column space of A. We project b onto the column space, and solve for Ax(hat) = p where p is the projection of b onto column space.

Andrew W
  • 1