Generally, what are the units of the second derivative?
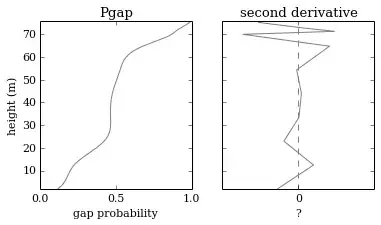
In this (very specific) example I have plotted height against gap probability, what should I put in place of the "?".
Generally, what are the units of the second derivative?
In this (very specific) example I have plotted height against gap probability, what should I put in place of the "?".

Consider the basic definition of a derivative according to Leibniz:
$$ \frac{d}{dx} f(x)\Big|_{x=x_0} = \lim_{x\rightarrow x_0}\frac{f(x)-f(x_0)}{x-x_0} $$
From this you see that if $f(x)$ has unit $u$, and $x$ has unit $v$, the derivative has unit $\frac{u}{v}$.
More generally, the $n$-th derivative $\frac{d^n}{dx^n} f(x)$ has unit $\frac{u}{v^n}$ (this is easily shown by repeating the above argument).
EDIT: In addition to the mathematics consider a basic example: let a function $s(t)$ denote the distance travelled by a car versus time, i.e. $s(t)$ has unit meters $m$ and the time $t$ has unit seconds $s$. The first derivative then has unit $m/s$ and descibes the velocity=distance per time. The second derivative has unit $m/s^2$ and describes acceleration, which is [change in velocity] per time.
Translated to your graph, the first derivative corresponds to [change in gap probability per height] or [slope of gap probability]. The sought second derivate then denotes [change in [slope of gap probability] per height]