I am trying to understand how to obtain $p$-values for the one-sided Kolmogorov-Smirnov test, and am struggling to find CDFs for $D^{+}_{n_{1},n_{2}}$ and $D^{-}_{n_{1},n_{2}}$ in the two-sample case. The below is cited in a few places as the CDF for $D^{+}_{n}$ in a one-sample case:
$$p^{+}_{n}\left(x\right) = \text{P}\left(D^{+}_{n} \ge x | \text{H}_{0}\right) = x\sum_{j=0}^{\lfloor n\left(1-x\right)\rfloor}{ \binom{n}{j} \left(\frac{j}{n}+x\right)^{j-1}\left(1 - x - \frac{j}{n}\right)^{n-j}}$$
Also, whuber sez there's a slightly different formulation of this one-sample CDF (I am substituting $x$ for $t$ in his quote for consistency with my notation here):
Using the probability integral transform, Donald Knuth derives their (common) distribution on p. 57 and exercise 17 of TAoCP Volume 2. I quote:
$$\left(D^{+}_{n}\le \frac{x}{\sqrt{n}}\right)=\frac{x}{n^{n}}\sum_{c\le k\le x}\binom{n}{k}\left(k-x\right)^{k}\left(x+n-k\right)^{n-k-1}$$
This would apply to one-sided hypotheses in the one-sample case, such as: H$_{0}\text{: }F(x)-F_{0} \le 0$, where $F(x)$ is the empirical CDF of $x$, and $F_{0}$ is some CDF.
I think the $x$ in this case is the value of $D^{+}_{n}$ in one's sample, and that $\lfloor n\left(1-x\right)\rfloor$ is the largest integer in $n-nx$. (Is that right?)
But what is the CDF for $D^{+}_{n_{1},n_{2}}$ (or $D^{-}_{n_{1},n_{2}}$) when one has two samples? For example, when H$_{0}\text{: }F_{A}(x)-F_{B}(x) \le 0$ for the empirical CDFs of $A$ and $B$? How to obtain $p^{+}_{n_{1},n_{2}}$?
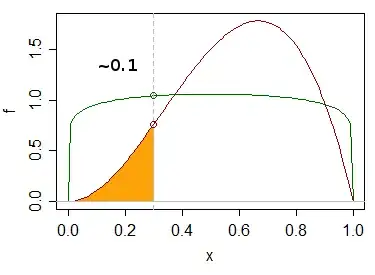
 $D^{+}$ (or
$D^{+}$ (or