I like the other answers, but nobody has mentioned the following yet. The event $\{U \leq t,\ V\leq t \}$ occurs if and only if $\{\mathrm{max}(U,V)\leq t\}$, so if $U$ and $V$ are independent and $W = \mathrm{max}(U,V)$, then $F_{W}(t) = F_{U}(t)*F_{V}(t)$ so for $\alpha$ a positive integer (say, $\alpha = n$) take $X = \mathrm{max}(Z_{1},...Z_{n})$ where the $Z$'s are i.i.d.
For $\alpha = 1/n$ we can switcheroo to get $F_{Z} = F_{X}^n$, so $X$ would be that random variable such that the max of $n$ independent copies has the same distribution as $Z$ (and this would not be one of our familiar friends, in general).
The case of $\alpha$ a positive rational number (say, $\alpha = m/n$) follows from the previous since
$$
\left(F_{Z}\right)^{m/n} = \left(F_{Z}^{1/n}\right)^{m}.
$$
For $\alpha$ an irrational, choose a sequence of positive rationals $a_{k}$ converging to $\alpha$; then the sequence $X_{k}$ (where we can use our above tricks for each $k$) will converge in distribution to the $X$ desired.
This might not be the characterization you are looking for, but it least gives some idea of how to think about $F_{Z}^{\alpha}$ for $\alpha$ suitably nice. On the other hand, I'm not really sure how much nicer it can really get: you already have the CDF, so the chain rule gives you the PDF, and you can calculate moments till the sun sets...? It's true that most $Z$'s won't have an $X$ that's familiar for $\alpha = \sqrt{2}$, but if I wanted to play around with an example to look for something interesting I might try $Z$ uniformly distributed on the unit interval with $F(z) = z$, $0<z<1$.
EDIT: I wrote some comments in @JMS answer, and there was a question about my arithmetic, so I'll write out what I meant in the hopes that it's more clear.
@cardinal correctly in the comment to @JMS answer wrote that the problem simplifies to
$$
g^{-1}(y) = \Phi^{-1}(\Phi^{\alpha}(y)),
$$
or more generally when $Z$ is not necessarily $N(0,1)$, we have
$$
x = g^{-1}(y) = F^{-1}(F^{\alpha}(y)).
$$
My point was that when $F$ has a nice inverse function we can just solve for the function $y = g(x)$ with basic algebra. I wrote in the comment that $g$ should be
$$
y = g(x) = F^{-1}(F^{1/\alpha}(x)).
$$
Let's take a special case, plug things in, and see how it works. Let $X$ have an Exp(1) distribution, with CDF
$$
F(x) = (1 - \mathrm{e}^{-x}),\ x > 0,
$$
and inverse CDF
$$
F^{-1}(y) = -\ln(1 - y).
$$
It is easy to plug everything in to find $g$; after we're done we get
$$
y = g(x) = -\ln \left( 1 - (1 - \mathrm{e}^{-x})^{1/\alpha} \right)
$$
So, in summary, my claim is that if $X \sim \mathrm{Exp}(1)$ and if we define
$$
Y = -\ln \left( 1 - (1 - \mathrm{e}^{-X})^{1/\alpha} \right),
$$
then $Y$ will have a CDF which looks like
$$
F_{Y}(y) = \left( 1 - \mathrm{e}^{-y} \right)^{\alpha}.
$$
We can prove this directly (look at $P(Y \leq y)$ and use algebra to get the expression, in the next to the last step we need the Probability Integral Transform). Just in the (often repeated) case that I'm crazy, I ran some simulations to double-check that it works, ... and it does. See below. To make the code easier I used two facts:
$$
\mbox{If $X \sim F$ then $U = F(X) \sim \mathrm{Unif}(0,1)$.}
$$
$$
\mbox{If $U \sim \mathrm{Unif}(0,1)$ then $U^{1/\alpha} \sim \mathrm{Beta}(\alpha,1)$.}
$$
The plot of the simulation results follows.
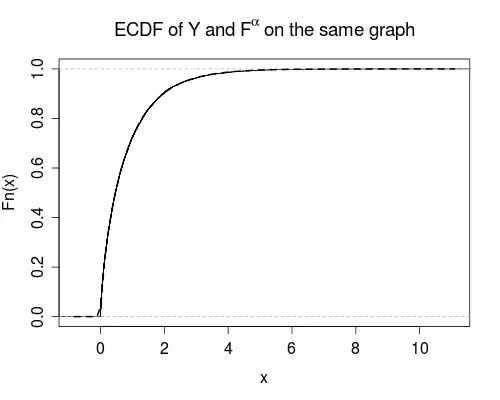
The R code used to generate the plot (minus labels) is
n <- 10000; alpha <- 0.7
z <- rbeta(n, shape1 = alpha, shape2 = 1)
y <- -log(1 - z)
plot(ecdf(y))
f <- function(x) (pexp(x, rate = 1))^alpha
curve(f, add = TRUE, lty = 2, lwd = 2)
The fit looks pretty good, I think? Maybe I'm not crazy (this time)?