1

suppose that we have following data

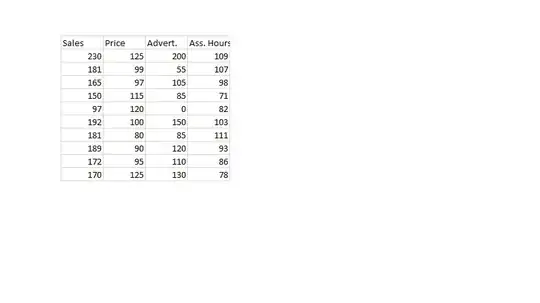
enter image description here

i have done covariance matrix and eigenvalue decomposition

>> means=mean(X);
>> centered=X-repmat(means,10,1);
>> covariance=(centered'*centered)/(9);

>> [V,D]=eig(covariance);
>> [e,i]=sort(diag(D),'descend');
>> sorted=V(:,i);

e

e =

   1.0e+03 *

    3.8861
    0.4605
    0.1162
    0.0465

>> sorted

sorted =

    0.5080    0.5042    0.3747   -0.5893
    0.0090   -0.6091    0.7930   -0.0092
    0.8560   -0.3490   -0.2747    0.2647
    0.0955    0.5030    0.3941    0.7633

i have calculated also percentage distribution

(e./sum(e))*100

ans =

   86.1796
   10.2125
    2.5776
    1.0303

for instance i want to choose first two,because in sum they have more then 96% of total variance,now please how can i continue for factor analysis?matlab commands also visual help will be very good,according to this answer

Steps done in factor analysis compared to steps done in PCA

i was confused,so please for given concrete numerical example,how can i continue,not just definitions,i need concrete numerical steps.thansk in advance

EDITED : because i have choose first two eigenvector,i have done PCA also

factors=sorted(:,1:2)

factors =

    0.5080    0.5042
    0.0090   -0.6091
    0.8560   -0.3490
    0.0955    0.5030

>> PCA=X*factors

PCA =

  299.5739   24.8602
  150.1380   65.5846
  183.9319   36.7606
  156.7749   11.6325
   58.1864   17.0585
  236.6723   35.3584
  176.0291   68.7008
  208.4237   45.3761
  190.6039   33.7278
  206.2131    3.4430

how can i calculate loadings?how can i do orthogonal rotations?

Community
  • 1
dato datuashvili
  • 723
  • 2
  • 7
  • 21

1 Answers1

2

Good news! You've allready calculated the loadings. The loadings are the weight each observation gets in the principal components. What you call 'factors' are the 'factor loadings'.

Rotations are performed on these 'loadings'=='eigenvectors'. The method to do this is dependent on the type of (ortoghonal) rotation you intend to do. The stats package has pca() and rotatefactors() (link) methods it that package is available to you.

Sidenote: I see that you calculated the eigenvectors with the covariance matrix, this assumes that all data is in the same scale. That is variations in Hours have the same impact as variations in Price. It might be more informative to use the eigenvalues of the correlation matrix corrcoef().

I also see that a lot of your coding is "reinventing the wheel" maybe thats intentional to learn but for example covariance matrices are built in in base via var(X) (link).

Good luck!

Community
  • 1
Walter
  • 236
  • 1
  • 4
  • 1
    `The loadings are the weight each observation gets in the principal components` What do you mean? – ttnphns Jun 22 '14 at 07:07
  • what I mean is that a matrix $K \times N$ of observations of the variables with rows $X_i =$ `[Sales, Price, Advert., Ass. Hours]`_i (i=1..N) which we're trying to reduce using `PCA` is weighted by loadings (eigenvectors) $V_1 .. V_K$ (each of length $K$) to form principal component $k$ row $i$ according to ${PCA}_{ik}= \sum_{\kappa=1}^K X_{i\kappa} \cdot V_{\kappa k}$. Hope the math is ok :) – Walter Jun 22 '14 at 08:16
  • thanks for your answer,just i want to see formula of rotation,what is rotational matrix in this case – dato datuashvili Jun 22 '14 at 17:11
  • That's dependant on the type of rotation you would like to perform. As the eigenvectors are by definition orthogonal, every orthogonal rotation matrix will do. Typically this is an optimization. Varimax is fairly standard https://en.wikipedia.org/wiki/Varimax_rotation – Walter Jun 22 '14 at 20:13
  • ok but that step is very interesting for me,i have got loadings right,no what i should do?should i multiply this matrix by some orthogonal matrix or?ok simple mathematical formula for it,let say Varimax – dato datuashvili Jun 23 '14 at 10:18
  • $PC = \text{eigenvector}(\text{cov}(X))$; $R_{Varimax}\cdot PC = RC$; $X\cdot RC$ – Walter Jun 23 '14 at 12:37
  • sorry what is RC?in this case what is form of Rvarimax? – dato datuashvili Jun 24 '14 at 17:23