Solution
Generate these numbers using the probability integral transform.
When $F$ is any cumulative distribution function and it is truncated at values $t_0 \lt t_1$, then random values can be obtained as
$$X = F^{-1}(U)$$
where $U$ is uniformly distributed in the interval $[a,b]=[F(t_0), F(t_1)]$. In this case $F^{-1}$ can be computed explicitly (even by Excel).
Implementation Details
Due to the notorious and long-standing deficiencies in Excel's documentation and computations, I never use its lognormal functions: as a policy, I use only the most basic function that will get the job done. This minimizes the amount of testing that needs to be performed in order to establish reliable results and maximizes the chance that I correctly understand what the software is doing.
In this case, everything can be handled with the CDF $\Phi$ and inverse CDF $\Phi^{-1}$ of the standard normal distribution. (Excel's names for these are NORMSDIST and NORMSINV, respectively.) For a lognormal distribution of mean $m$ and standard deviation $s$, compute
$$\sigma = \log\left(1 + \left(\frac{s}{m}\right)^2\right)$$
and then
$$\mu = \log(m) - \sigma^2/2.$$
These are the standard deviation and mean, respectively, of the distribution of the logarithms of the values. In these terms
$$F(x) = \Phi\left(\frac{\log(x) - \mu}{\sigma}\right)$$
and
$$F^{-1}(q) = \exp\left(\mu + \sigma \Phi^{-1}(q)\right).$$
In Excel--as well as in many other software platforms--a uniform random value $U$ in an interval $[a,b]$ is generated by obtaining a random variate $V$ from the interval $[0,1]$--which is produced by Excel's RAND function--and rescaling it:
$$U = a + (b-a)V.$$
Excel Implementation
In addition to the usual arithmetic operations (addition, multiplication, etc) this calculation relies on only four functions: RAND, NORMSDIST, NORMSINV, and LN. The first three have well-known problems (but there's no workaround for them short of recoding them in VBA). Nevertheless, for the small simulations that Excel can handle RAND will be fine--especially when using more recent versions of Excel--and the errors in NORMSDIST and NORMSINV (which occur way out in the tails) are unlikely to be encountered.
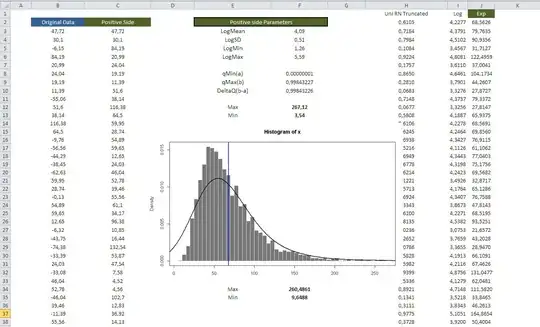
The screen shot displays a portion of spreadsheet in which 256 random variates X (in column C) are generated according to the specifications at its right: Mean, SD, Min, and Max. These are the only inputs to the calculation. The bars in the chart tally one realization of these variates while the solid line is the graph of the truncated probability density function (rescaled to show the expected counts in each bin). The deviations between the bar heights and the graph are due to random variation only. (Notice how level the graph is: in this particular example the truncated lognormal distribution could be closely approximated by a simple uniform distribution.)
All values in the Value column are referenced by names derived from the Parameter column. The formulas are:
LogMean represents $\mu$: =LN(Mean) - LogSD^2/2
LogSD: represents $\sigma$: =LN(1 + SD^2/Mean^2).
LogMin is the logarithm of the left endpoint of the truncation interval: =LN(Min)
LogMax is the logarithm of the right endpoint of the truncation interval: =LN(Max)
qMin is $a$, the lower limit of the quantile $U$: =NORMSDIST((LogMin - LogMean)/LogSD)
qMax is $b$, the upper limit of $U$: =NORMSDIST((LogMax-LogMean)/LogSD)
DeltaQ is $b-a$ for the calculation of $U$: =qMax-qMin.
The entries in columns A:C are each obtained by a formula entered at the first row and copied down:
Uniform RN represents $U$, computed as =qMin + DeltaQ*RAND().
Y are the logarithms of the random values, computed as =LogMean + LogSD * NORMSINV(A2) et seq.
X is obtained by exponentiating Y: =EXP(B2), et seq.