21

I am trying to put together a data-mining package for StackExchange sites and in particular, I am stuck in trying to determine the "most interesting" questions. I would like to use the question score, but remove the bias due to the number of views, but I don't know how to approach this rigorously.

In the ideal world, I could sort the questions by calculating $\frac{v}{n}$, where $v$ is the votes total and $n$ is the number of views. After all it would measure the percentage of people that upvote the question, minus the percentage of people that downvote the question.

Unfortunately, the voting pattern is much more complicated. Votes tend to "plateau" to a certain level and this has the effect of drastically underestimating wildly popular questions. In practice, a question with 1 view and 1 upvote would certainly score and be sorted higher than any other question with 10,000 views, but less than 10,000 votes.

I am currently using $\frac{v}{\log{n}+1}$ as an empirical formula, but I would like to be precise. How can I approach this problem with mathematical rigorousness?

In order to address some of the comments, I'll try to restate the problem in a better way:

Let's say I have a question with $v_0$ votes total and $n_0$ views. I would like to be able to estimate what votes total $v_1$ is most likely when the views reach $n_1$.

In this way I could simply choose a nominal value for $n_1$ and order all the question according to the expected $v_1$ total.

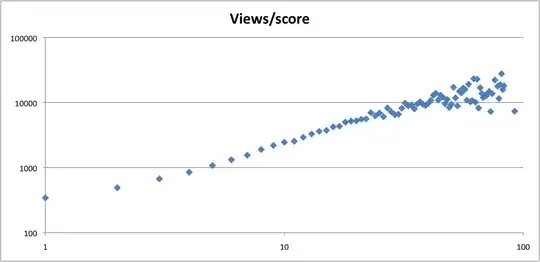
I've created two queries on the SO datadump to show better the effect I am talking about:

Average Views by Score

Result:

Views by Score

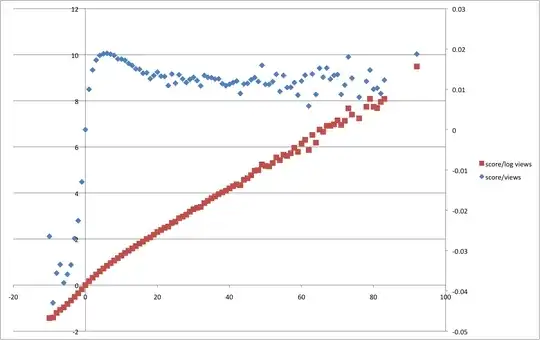
Average Score by Views (100-views buckets)

Result:

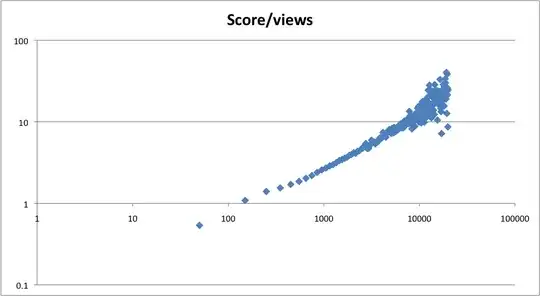
Score by Views

The two formulas compared

Results, not sure if straighter is better: ($\frac{v}{n}$ in blue, $\frac{v}{log{n}+1}$ in red)

Formulas

Sklivvz
  • 393
  • 3
  • 11
  • This certainly is an interesting question, but I think you might be better off asking this on stats.SE. –  May 03 '11 at 22:05
  • @Theo You may be right, actually. I'll flag for the mods to migrate if they think it's best. –  May 03 '11 at 22:08
  • 1
    Why would views not contribute to interesting-ness? (but worse, why would they contribute negatively?) More interesting things tend to be viewed more often... The fundamental problem here is what does _interesting_ even mean? Does it means questions of general _interest_ or questions that are of interest to a more specific higher level audience? For someone to answer this question with "mathematical rigourousness", it needs to be posed rigorously first. –  May 03 '11 at 22:11
  • Views bias the questions because one question might, say, be link by a good site and receive tons of views--if you look at the [top rated questions](http://math.stackexchange.com/questions?sort=votes) they are all high view questions; by interesting I mean the questions that have more value as perceived by the users of the site. In any case, the question still stands: what is the correct way of combining views and votes to get the best predictor of quality? –  May 03 '11 at 22:14
  • **[Here](http://stats.stackexchange.com/questions/9885/application-of-machine-learning-methods-in-stackexchange-websites)** is a recent somewhat-related question to yours, though the answers won't be relevant. – cardinal May 03 '11 at 22:22
  • 2
    The math people asked good questions. This question's logic seems circular: it appears to ask us for a formula to measure the "quality" of an SE question but it doesn't stipulate what "quality" means except to give non-operational synonyms like "value as perceived by the users of the site." You can't get something for nothing! – whuber May 03 '11 at 22:29
  • @whuber: hopefully I've addressed your concerns in the question. – Sklivvz May 03 '11 at 22:36
  • @Skl: Much better! – whuber May 03 '11 at 22:38
  • I don't really understand why views has anything to do with this, since a post can have an interesting title and be totally uninteresting; not to mention linking etc...For example if I look over my own questions that I have posted, I find that the best ones have the most upvotes, and that the view total is basically reflects other factors. – Matt May 03 '11 at 22:49
  • @Matt: Well, first of all views limit the top score, $v – Sklivvz May 03 '11 at 22:54
  • I'd imagine that _many_ people are trying to do what you are trying to do: come up with a way to predict "interestingness," including reddit, google, and yes, stackexchange... It would be worth taking a look at what they have considered. – charles.y.zheng May 04 '11 at 02:45
  • Do you have access to the "trajectory" of every question (i.e. score and #views at many time instants), or do you just have the current state? – SheldonCooper May 04 '11 at 19:07
  • What do you mean by the "trajectory"? Something I could use to plot a view/vote scatter for each question? – Sklivvz May 04 '11 at 21:16
  • I meant how the number of views and the vote count changes with time. When it starts out, #views = 0 and #votes = 0. Then it goes to "1 views, 0 votes", then, say, to "2 views, 0 votes", then to "3 views, 1 vote", etc., until it reaches the present state of "100 views, 10 votes". – SheldonCooper May 05 '11 at 00:48

2 Answers2

3

One might define an interesting question as one that has received comparatively many votes given the number of views. To this end, you can create a baseline curve that reflects the expected number of votes given the views. Curves that attracted a lot more votes than the baseline were considered particularly interesting.

To construct the baseline, you may want to calculate the median number of votes per 100-view bin. In addition, you could calculate the median absolute deviation (MAD) as a robust measure for the standard deviation per bin. Then, "interestingness" can be calculated as 

interestingness(votes,views) = (votes-baselineVotes(views))/baselineMAD(views)
Jonas
  • 1,578
  • 1
  • 13
  • 16
  • Probably also want *time* in the definition since the same interestingness score you propose for a question three years old means a very different thing than for a question three hours old. – Alexis Jan 06 '20 at 20:04
1

This is my theory. I think there are two kinds of questions: those that remain mostly within SE (which usually have fewer views), and those that are viewed by outsiders because it was linked from somewhere else (usually have more views).

For the questions that remain mostly within SE, votes are a good measure of interesting questions. This is the point of votes.

When a question is linked to outside the site the votes stop meaning as much. Some linking sites may have very few SE members, others may have more. The variance of the number of votes for these questions is probably high (as evidenced by your score vs view plot, where the right side of the curve blooms out). These questions will have more views, and views MAY be a better indicator of interesting questions. Or questions that a larger community happened to find more interesting. There are many variables in this situation, and I think it would be worth trying to find more information to differentiate these cases. Does SE publicize referral information?

rm999
  • 748
  • 5
  • 10
  • Does SE publicize referral information? I'd be interested to know the viewing pattern of posts rather than just upvotes, comments, etc. – d_a_c321 Nov 23 '11 at 21:46