I'm looking for linear regression algorithm that is most suitable for a data whose independent variable (x) has a constant measurement error and the dependent variable (y) has signal dependent error.
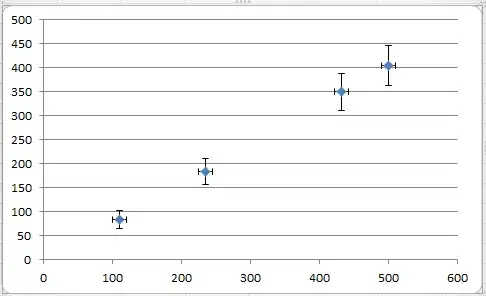
The above image illustrates my question.
I'm looking for linear regression algorithm that is most suitable for a data whose independent variable (x) has a constant measurement error and the dependent variable (y) has signal dependent error.

The above image illustrates my question.
Measurement error in the dependent variable
Given a general linear model $$y=\beta_0+\beta_1 x_1+\cdots+\beta_kx_k+\varepsilon\tag{1}$$ with $\varepsilon$ homosckedastic, not autocorrelated and uncorrelated with the independent variables, let $y^*$ denote the "true" variable, and $y$ its observable measure. The measurement error is defined as their difference $$e=y-y^*$$ Thus, the estimable model is: $$y=\beta_0+\beta_1 x_1+\cdots+\beta_kx_k+e+\varepsilon\tag{2}$$ Since $y,x_1,\dots,x_k$ are observed, we can estimate the model by OLS. If the measurement error in $y$ is statistically independent of each explanatory variable, then $(e+\varepsilon)$ shares the same properties as $\varepsilon$ and the usual OLS inference procedures ($t$ statistics, etc.) are valid. However, in your case I'd expect an increasing variance of $e$. You could use:
a weighted least squares estimator (e.g. Kutner et al., §11.1; Verbeek, §4.3.1-3);
the OLS estimator, which is still unbiased and consistent, and heteroskedasticity-consistent standard errors, or simply Wite standard errors (Verbeek, §4.3.4).
Measurement error in the independent variable
Given the same linear model as above, let $x_k^*$ denote the "true" value and $x_k$ its observable measure. The measurement error is now: $$e_k=x_k-x_k^*$$ There are two main situations (Wooldridge, §4.4.2).
$\text{Cov}(x_k,e_k)=0$: the measurement error is uncorrelated with the observed measure and must therefore be correlated with the unobserved variable $x^*_k$; writing $x_k^*=x_k-e_k$ and plugging this into (1): $$y=\beta_0+\beta_1x_1+\cdots+\beta_kx_k+(\varepsilon-\beta_ke_k)$$ since $\varepsilon$ and $e$ both are uncorrelated with each $x_j$, including $x_k$, measurement just increases the error variance and violates none of the OLS assumptions;
$\text{Cov}(x^*_k,\eta_k)=0$: the measurement error is uncorrelated with the unobserved variable and must therefore be correlated with the observed measure $x_k$; such a correlation causes prolems and the OLS regression of $y$ on $x_1,\dots,x_k$ generally gives biased and unconsitent estimators.
As far as I can guess by looking at your plot (errors centered on the "true" values of the independent variable), the first scenario could apply.