What are some examples of a mathematical result being counterintuitive?

Question

As I procrastinate studying for my Maths Exams, I want to know what are some cool examples of where math counters intuition.

My first and favorite experience of this is Gabriel's Horn that you see in intro Calc course, where the figure has finite volume but infinite surface area (I later learned of Koch's snowflake which is a 1d analog). I just remember doing out the integrals for it and thinking that it was unreal. I later heard the remark that you can fill it with paint, but you can't paint it, which blew my mind.

Also, philosophically/psychologically speaking, why does this happen? It seems that our intuition often guides us and is often correct for "finite" things, but when things become "infinite" our intuition flat-out fails.

Answer 1

Here's a counterintuitive example from The Cauchy Schwarz Master Class, about what happens to cubes and spheres in high dimensions:

Consider a n-dimensional cube with side length 4, $B=[-2,2]^n$, with radius 1 spheres placed inside it at every corner of the smaller cube $[-1,1]^n$. Ie, the set of spheres centered at coordinates $(\pm 1,\pm 1, \dots, \pm 1)$ that all just barely touch their neighbor and the wall of the enclosing box. Place another sphere $S$ at the center of the box at 0, large enough so that it just barely touches all of the other spheres in each corner.

Below is a diagram for dimensions n=2 and n=3.

Does the box always contain the central sphere? (Ie, $S \subset B$?)

Surprisingly, No! The radius of the blue sphere $S$ actually diverges as the dimension increases, as shown by the simple calculation in the following image,

The crossover point is dimension n=9, where the central sphere just barely touches the faces of the red box, as well as each of the 512(!) spheres in the corners. In fact, in high dimensions nearly all of the central sphere's volume is outside the box.

Answer 2

It's somewhat counterintuitive that simple symmetric random walks in 1 dimension and in 2 dimensions return to the origin with probability 1.

Once one has absorbed that fact, it may be somewhat counterintuitive that the same thing is not true in higher dimensions.

(see Proving that $1$- and $2D$ simple symmetric random walks return to the origin with probability $1$, Examples of results failing in higher dimensions, and Pólya's Random Walk Constant)

Answer 3

As some other people said, "intuition is highly subjective". Different people think about problems in different ways.

That said, there are many, many counter-intuitive results in mathematics. This is why people demand rigorous proof! ;-)

• Almost any result involving probability. Humans suck at probability! (E.g., the birthday paradox: The probability that anyone in the room shares the same birthday as you is very small, unless you have a lot of people. But the probability that anybody in the room shares a birthday is very high. Way higher than you'd imagine...)

• Almost any result involving infinite sets. Infinity doesn't behave how you'd expect at all! ("Infinity" actually comes in different sizes. $\mathbb{Q}$ is the same size as $\mathbb{N}$, despite being a superset of it. Subtracting an infinite set from an infinite set can yield a result of positive finite size. Etc.)

• Several results about things which are impossible to compute. (E.g., the halting problem looks like it should be really, really easy, but it's actually impossible. Rice's theorem also sounds completely ludicrous. The busy beaver function is non-computable, regardless of how easy it looks. And so forth.)

• Fractal geometry contains a few results which break people's minds. (E.g., polygon which has infinity perimeter and zero area. A Julia set where every point simultaneously touches three basins of attraction. A connected curve with no derivatives...)

I could probably think of more, given enough time...

Answer 4

The topological manifold $\mathbb{R}^n$ has a unique smooth structure up to diffeomorphism... as long as $n \neq 4$.

However, $\mathbb{R}^4$ admits uncountably many exotic smooth structures.

Answer 5

The Monty Hall Problem is another finite example which most people find highly counter-intuitive. I believe even Erdos refused to believe its solution was correct for a while.

Answer 6

It is possible to define a curve which fills every point of a two-dimensional square (or, more generally, an $n$-dimensional hypercube). Such curves are called space-filling curves, or sometimes Peano curves.

More precisely, there is a continuous surjection from the interval $I$ onto the square $I\times I$.

This is related to the (also counter-intuitive?) result of Cantor, that the cardinality of the number of points in the unit interval is the same as the that of the unit square, or indeed any finite-dimensional manifold.

Answer 7

Suppose we are tossing a fair coin. Then the expected waiting time for heads-heads is 6 throws, but the expected waiting time for tails-heads is 4 throws. This is very counterintuitive to me because the events heads-heads and tails-heads has the same probability, namely $\tfrac{1}{4}$. The general result is the following:

Suppose we are throwing a coin that has probability $p$ for heads and probability $q=1-p$ for tails. Let $V_{\text{HH}}$ be first time we encounter two heads in a row and $V_{\text{TH}}$ be the first time we encounter heads and tails in a row, i.e. $$ V_{\text{HH}}(\omega)=\min\{n\geq 2\mid \omega\in H_{n-1}\cap H_n\},\\ V_{\text{TH}}(\omega)=\min\{n\geq 2\mid \omega\in H_{n-1}^c\cap H_n\}, $$ where $H_n$ is the event that we see heads in the $n$'th throw. Then $$ E[V_{\text{HH}}]=\frac{1+p}{p^2},\\ E[V_{\text{TH}}]=\frac{1}{pq}. $$ Putting $p=q=\tfrac{1}{2}$ we see that if our coin is a fair coin then $E[V_{\text{HH}}]=6$ and $E[V_{\text{TH}}]=4$.

Answer 8

Whether something is intuitive or counterintuitive is a very subjective matter. Lots of results are counterintuitive if you don't have the correct intuition. But here's one elementary result of my own that you may find counterintuitive.

Suppose $N$ players are to conduct a knockout tournament. Their starting positions, on the leaves of a rooted binary tree, are chosen randomly, all such assignments being equally likely. When two players are at the children of an unoccupied node, they play a game and the winner (ties are not allowed) advances to that node. The winner of the tournament is the player who reaches the root. We assume that in any game between two given players $i$ and $j$, the probability that $i$ wins is a given number $p_{ij}$, independent of past history. These probabilities are assumed to satisfy strong stochastic transitivity, which means that if $p_{ij} \ge 1/2$ then $p_{ik} \ge p_{jk}$ for all $k$, i.e. if $i$ wins against $j$ at least half the time, then $i$ does at least as well as $j$ against any other player. Thus the probabilities $p_{ij}$ generate a consistent ordering of the players by ability.

Now it seems intuitive that under these conditions, better players have a better chance of winning the tournament. Indeed, it was conjectured that this was the case. However, it is not true, as I proved: "Stronger Players Need Not Win More Knockout Tournaments", Journal of the American Statistical Association 76 (1981) 950-951: https://doi.org/10.1080/01621459.1981.10477747

Answer 9

Choose a natural number, for example $n=8$. Then pick a base, for example $b=2$, and finally select another natural number called the bump factor, for example $B=1000$. Then construct a sequence of natural numbers as follows: The first term of the sequence is simply $n$ written in expanded base $b$. $$m_{0}=2^{2+1}=8$$ The second term is obtained from the first by bumping the base $b$ by a factor of $B$ and then subtracting $1$ from the result. $$m_{1}=2000^{2000+1}-1=\sum_{k=0}^{2000}1999\cdot2000^{k}>10^{10^3}$$ The third term is obtained from the second by bumping the new base ($2000$) by a factor of $B$ and then subtracting $1$ from the result. Denoting $d=2\cdot 10^{6}$ we have $$m_{2}=1999d^{d}+1999d^{1999}+\cdots+1999d+1998>10^{10^7}$$ Continuing in this fashion we denote $e=2\cdot10^{9}$ and the next term is $$m_{3}=1999e^{e}+1999e^{1999}+\cdots+1999e+1997>10^{10^{10}}.$$ The next term $m_{5}$ has over 24 trillion decimal digits.

Intuition tells us that the sequence $(m_{r})$ goes to infinity, and very fast. However, this is not the case. Surprisingly, the sequence will reach $0$ in finitely many steps. That is, there is an $r\in \mathbb{N}$ for which $m_{r}=0$.

The sequence we constructed is an example of a Goodstein sequence, and the fact that it terminates is a very particular case of Goodstein's Theorem. This theorem is counterintuitive for two reasons. First because of what the theorem concludes. Roughly speaking, it states that any sequence of natural numbers of the type constructed above (i.e. a Goodstein sequence) will always terminate. Second, because of what it is required to prove it. Goodstein's theorem is a fairly elementary statement about natural numbers (i.e. formulated within the Peano Axioms of Arithemtic) and yet its proof cannot be carried out using only these axioms. It requires infinite ordinals.

Answer 10

I also Think The Kakeya Needle Problem is worth mentioning (see https://mathworld.wolfram.com/KakeyaNeedleProblem.html). To me it is counter-intuitive that there is no smallest set, in which a needle of unit length can be freely rotated. Unless it has to be convex, of course.

Answer 11

Just to throw in something different, it's pretty wild that Khinchin's constant is universal for almost every real number (except for rationals and a few other miscreants). By definition if $x$ has continued fraction $x=a_0+\frac{1}{a_1+\frac{1}{a_2+\ldots}}$, then for almost all $x$,
$\lim_{n\rightarrow\infty} (a_1a_2\cdots a_n)^{1/n}\approx 2.685$

Answer 12

Really interesting question, I have some examples that many people find counterintuitive.

The set $\mathbb Q$ of rational numbers as the same cardinality of the set of natural numbers $\mathbb N$, although $\mathbb N$ is strictly contained in $\mathbb Q$. Similarly many people find it to be counterintuitive that even numbers are equal in cardinality to the naturals (i.e. the sets $\{2n \mid n \in \mathbb N\}$ and $\mathbb N$ have the same cardinality).

The set $\mathbb R$ has cardinality strictly greater than the set $\mathbb N$ (and so also of the set $\mathbb Q$) (so there's not just one type of infinity).

Another good example of a counterintuitive fact is the Banach-Tarski paradox stating that a ball can be decomposed in a finite number of pieces which can be glued together to build up two balls identical to the first one (I say that this is a paradox because the axiom of choice is clearly true :D).

If other examples come to my mind I'll add them later.

Answer 13

Here are a few counter-intuitive results that have surprised me at one point or another:

1. Impossible Constructions using Straightedge and Compass. Not all regular $n$-gons are constructible with straightedge and compass.
2. Godel's Incompleteness Theorems. Certain non-trivial arithmetics cannot be both complete and consistent.
3. Exotic spheres. In certain dimensions there are spheres which are homeomorphic but not diffeomorphic to the standard sphere.
4. Kuratowski's Closure-Complement Theorem. The largest number of distinct sets obtainable by repeatedly applying closure and complement to a given starting subset of a topological space is 14.
5. Dehn's Answer to Hilbert's Third Problem. The cube and regular tetrahedron are not scissor-congruent.

Answer 14

Löb's or Curry's paradox:

If this sentence is true, then Germany borders China.

Logic says this means "Germany borders China" (or anything you want to put after the "then").

Answer 15

The existence of countable countably infinite connected Hausdorff spaces is (to me) counterintutive. (Just one example; I could think of others . . . . .)

Later edit: A Hausdorff space is a topological space in which, for every pair of points $x$ and $y$, there are open neighborhoods of $x$ and $y$ that do not intersect each others, i.e. $x$ and $y$ can be in a certain sense separated from each other.

A connected space is a topological space that cannot be broken into separate components having no proximity to each other. Imagine two disks remote from each other. No sequence of points in one disk can approach a point in the other as a limit. That's a space that is not connected.

Countable means either finite or countably infinite, as opposed to uncountably infinite, and that means one can list all the point in a sequence: $x_1,x_2,x_3,\ldots$. The sequence may be infinite, but each term in the sequence has only finitely many terms before it.

So figure out what a countable connected Hausdorff space is based on all that.

Answer 16

I didn't think of this until today, but it's an important thing that I, and many other people, find completely mindboggling.

Let's consider properties, like "is red" or "has kidneys" or "has a heart". Now there's a certain sense in which two properties might be the same even though they don't look the same, which is that they might be true of exactly the same entities. For example, it might turn out that everything that has kidneys also has a heart and vice versa, so that even though the two properties have different meanings (kidneys are not the same as hearts), they amount to the same thing in practice.

Mathematics is of course full of such properties; consider for example the property ${\mathcal O}_1$ of being expressible in the form $2n+1$ for some integer $n$, and the property ${\mathcal O}_2$ of being expressible in the form $S_{n+1} - S_n$ for some pair of consecutive squares. Many theorems are of this type, that two seemingly different properties are actually the same.

So let's try to abstract away the senses of properties, leaving only the classes of things that possess them. We'll say that there are these entities called sets which are abstractions of properties. Things belong to a set exactly if they possess the property of which the set is the extension:

1. For every property $P(x)$, there is a corresponding set $\{x : P(x)\}$ of exactly those entities $x$ for which $P(x)$ is true.

2. An entity $y$ is a member of a set $\{x : P(x)\}$ if, and only if, $P(y)$ is true.

That seems utterly straightforward and utterly unexceptionable, and yet, it is utterly wrong.

There are completely mundane properties for which there is no corresponding set of all the entities with the property.

What? Who ordered that?

Answer 17

There are a number of results of the form "Proposition P fails in dimension $d$" where P holds in lower dimensions, many of which can seem counterintuitive until you understand higher dimensional phenomena.

Here's an elementary one, which many people on this site won't find counterintuitive but some might. Consider the question "What is the maximum number of vertices a polyhedron in $\mathbb{R}^d$ can have such that there is a segment joining every pair of points which is an edge of the polyhedron?" For $d=2$, the answer is obviously 3, with a triange. It's not difficult to see that a tetrahedron is optimal for $d=3$. Intuition suggests that the $d$-simplex is optimal based on this.

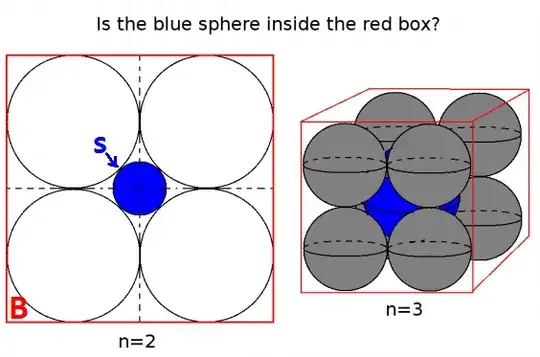
But for $d=4$, in fact, there is no maximum number. There are polyhedra in $\mathbb{R}^4$ with arbitrarily many vertices and an external edge joining each pair of vertices. If you take any finite collection of points on the moment curve $\{(t,t^2,t^3,t^4)\, | \, t>0\}$, the segment joining any two of the points is a face of the convex hull of the collection. Once you have an intuition for higher dimensional geometry, this is obvious, but it can seem counterintuitive.

A more advanced example, that I still find counterintuitive at times, is this: In $\mathbb{R}^d$ for $d=2,3$, given any polyhedron, one can move each of the vertices a small amount to obtain a combinatorially equivalent polyhedron with rational vertices. But in $d=4$ and higher there are polyhedra which can not be realized with rational coordinates.

EDIT: I was asked to provide a reference. This is a well-known result in some circles, particularly in computational geometry, so it's covered in a number of locations. Marcel Berger's Geometry Revealed covers both of the above so-called counterintuitive statements, as well as the surprisingly nonobvious case $d=3$, in chapter 8, roughly page 550, and is a pretty easy read. If you don't have access to Springer, the paper Realization spaces of polytopes by Richter-Gebert is the most comprehensive treatment I know of, and probably any book citing this paper is quoting the result.

Answer 18

A famous example of a counterintuitive fact in statistics is the James-Stein phenomenon. Suppose $X_1,\ldots,X_m$ are independent normally distributed random variables with expected values $\mu_1,\ldots,\mu_m$. One wishes to estimate $\mu_1,\ldots,\mu_m$ based on observation of $X_1,\ldots,X_m$. If instead of using $(X_1,\ldots,X_m)$ as the estimator of $(\mu_1,\ldots,\mu_m)$, one uses the James-Stein estimator $$ \left(1-\frac{(m-2)\sigma^2}{X_1^2+\cdots+X_m^2}\right)(X_1,\ldots,X_m) $$ (where $\sigma^2$ is the common variance) then the mean square error is smaller, regardless of the value of $(\mu_1,\ldots,\mu_m)$.

And the James-Stein estimator is demonstrably not even an admissible estimator, in the decision-theoretic sense. Thus the obvious estimator is inferior to one that is inferior to some admissible estimators.

One is "shrinking toward the origin", and it should be apparent that it doesn't matter which point you take to be the origin. In practice one should take the point toward which one shrinks to be the best prior guess about the value of $(\mu_1,\ldots,\mu_n)$.

The reason for the non-admissibility is that sometimes $(m-1)\sigma^2/(X_1^2+\cdots+X_n^2)$ is more than $1$, so that the sign gets reversed. That's too extreme by any standards. A piecewise-defined estimator that shrinks toward the origin but no further than the origin is superior in the mean-squared-error sense.

In the '80s and '90s, Morris L. Eaton showed that the fact that this works if $m\ge 3$ but not if $m\le2$ (apparent from the "$m-2$" in the numerator) is really the same fact as the fact that random walks are recurrent in dimension $\le2$ and transient in dimension $\ge 3$, which I think was discovered about a hundred years ago.

Answer 19

Another elementary example: Connelly spheres, also known as flexible polyhedra. These are non-convex polyhedra, homeomorphic to a sphere, with triangular faces; the polyhedra can be deformed continuously, while the faces remain rigid. It took about 211 years to find a counterexample to Euler's conjecture that embedded polyhedra are rigid. See e.g. http://www.reocities.com/jshum_1999/polyhedra/introduction.htm

Answer 20

Although well-known, I feel compelled to note the remarkable equation

$$ e^{i\pi} + 1 = 0. $$

That five of mathematics most well-known quantities are related in such a pleasantly simple way is astonishing and, to the the uninitiated, is certainly not intuitive. Of course, once one knows about infinite series, their basic properties and how to define the trigonometric and exponential functions with them, deriving this equation is routine. But, without this knowledge, the above equation seems almost mystical. In fact, this equation is what first piqued my own interest in mathematics.

Answer 21

I think Smale's paradox (sphere eversion) is pretty counterintuitive.

Video: https://www.youtube.com/watch?v=R_w4HYXuo9M

Also check out Wikipedia's list of mathematical paradoxes. ("'Paradox' here has the sense of 'unintuitive result', rather than 'apparent contradiction'.")

Answer 22

I think a puzzle at calculus level is the following: Given a real number $x$ and a conditionally convergent series, the series can be re-arranged so that its sum is $x$.

Answer 23

Intuition is a really subjective and personal matter. To go even further with the problem of such list is that there are many proof requiring some use of the axiom of choice. On the other hand, not assuming the axiom of choice can be equally reasonable, and here is a short list of how things might break down completely:

1. The real numbers can be a countable union of countable sets.
2. There might be no free ultrafilters, at all (on any set).
3. The rational numbers might have at least two non-isomorphic algebraic closures.
4. The natural numbers with the discrete topology might not be a Lindelof space.

Some results in ZFC which are completely unintuitive the first time you hear them:

1. While being perfectly definable, the set $\mathcal P(\mathbb N)$ can differ greatly between models of ZFC; or an even worse formulation:
2. There are models $M\subseteq N\subseteq V$ such that $N$ has more reals than $M$ and $V$ has more reals than $N$, but the amount of real numbers of $M$ and $V$ is the same.
3. There is a polynomial with integer coefficients which has a rational root if and only if ZFC is inconsistent.
4. Every model of ZFC is one class forcing from being $L[a]$ where $a$ is a real number; and every model is one set forcing away from being $HOD[A]$ for some set $A$.
5. The union of countably many disjoint open intervals might have uncountably many boundary points (e.g. the complement of the Cantor set in $[0,1]$).

Both lists are infinitely long, and I can probably ramble about the first list for several days. The point, as I say at first, is what we take for "granted" as intuitive which can change greatly between two people of different mathematical education; mathematical culture; and what is their usual axiomatic system (which is essential for "results").

---

One strange result on mathematicians is a direct corollary of the first result in the second list:

People are used to think that there is only one universe, only one fixed way to handle sets. While it is true that for the working mathematician this is often a reasonable approach, set theorists deal with models of set theory, much like group theorists deal with models of group theory.

Somehow everyone is flabbergasted when they are being told (for the first time, if not more) that there are many models of ZFC with different number of sets of natural numbers in each model; but no one falls of their chair when they are told that some fields have more irrational numbers than others...

Answer 24

The fact that one can easily prove the existence of uncountably infinite (as opposed to countably infinite) sets is counterintutive to me. Not that fact that uncountably infinite sets exist, but the fact that the proof is so simple. I was astonished when I first learned of it. I was in ninth grade. I think it was in a book by Vilenkin that I read the proof.

Similarly the fact that one can easily prove that the square root of $2$ is irrational. I hadn't expected that to be so simple. And the mere existence of irrational numbers seems counterintuitive: why shouldn't fractions be enough to fill up all the space between integers?

Answer 25

The fact that for any infinite set $A$ there is a bijection between $A$ and $A \times A$ is very counterintuitive for me...

Answer 26

I think the following has (suprisingly) not been pointed out already:

https://en.wikipedia.org/wiki/List_of_paradoxes#Mathematics

As a general rule paradoxes (counterintuitive truths) are very important in mathematics and there are many books dedicated to them. 1 and 2 are famous examples. The Monty Hall problem and Banach-Tarski paradox even have books dedicated to them, and each is the subject of ongoing research.

Paradoxes arise when simplification does not work, when usual assumptions do not hold. Of course this will depend on the person thinking about the phenomenon, on her experience. A topologist is well aware of counterexamples in her field so she would not find them paradoxical anymore.

Also I am not sure the Blue-eyed Islanders Paradox has been mentioned here. It has received much internet attention recently, foremost thanks to Terence Tao, c.f. also xkcd.

Answer 27

The concentration of measure phenomena on the sphere:

If $A\subset\mathcal{S}^{n-1}$ is a measurable set on the sphere with $\lambda(A)=1/2$ and $A_\epsilon$ is an epsilon neighborhood of $A$ on $\mathcal{S}^{n-1}$, then

$$\lambda(A_\epsilon)\geq 1-\frac{2}{e^{n\epsilon^2/2}}$$

So say you take $A$ to be a cap on the sphere and fix a small $\epsilon$. As the dimension of the sphere increases, eventually the $\epsilon$ enlargement of $A$ will have almost the entire area of the sphere! Playing with the upper and lower cap and the corresponding enlargements, one sees that area is concentrated around the equator.

Imagine you have a lawnmower and you cut the grass moving along the equator. What percentage of the sphere do you mow? Well, in 3 dimensions, not that much. But as you cut the grass on higher and higher dimensional spheres, moving centered along the equator, the surface area covered becomes almost 100% of the entire area of the sphere!

This result felt pretty counter-intuitive to me the first time I saw it.

Answer 28

The Weierstrass function. It showed that a function can be continuous everywhere but differentiable nowhere. This was (and still is) counterintuitive.

Answer 29

Perhaps the Banach–Tarski paradox: Given a solid ball in 3‑dimensional space, there exists a decomposition of the ball into a finite number of non-overlapping pieces (i.e. subsets), which can then be put back together in a different way to yield two identical copies of the original ball. The reassembly process involves only moving the pieces around and rotating them, without changing their shape.

https://en.wikipedia.org/wiki/Banach%E2%80%93Tarski_paradox

Answer 30

How about the Löwenheim–Skolem theorem?

One of its consequences is that the field of real numbers has a countable model.

Answer 31

Another elementary one. There is a configuration of 30 convex bodies in 3-dimensional space with disjoint interiors that "cannot be taken apart with two hands". That is, it's impossible to split up the set of bodies into two nonempty subsets and, by a rigid motion, move one of the subsets away to infinity without disturbing a member of the second subset. See https://www.cs.ubc.ca/labs/imager/contributions/snoeyink/sculpt/theorem.html and https://doi.org/10.1007/BF02574386

Answer 32

Although Dan Brumleve and plm linked the list of paradoxes, the famous Braess's paradox deserves a special attention.

"For each point of a road network, let there be given the number of cars starting from it, and the destination of the cars. Under these conditions one wishes to estimate the distribution of traffic flow. Whether one street is preferable to another depends not only on the quality of the road, but also on the density of the flow. If every driver takes the path that looks most favorable to him, the resultant running times need not be minimal. Furthermore, it is indicated by an example that an extension of the road network may cause a redistribution of the traffic that results in longer individual running times."

Answer 33

This, is the most counterintuitive fact that I ever saw:

Blue Eyes Islanders Question: https://www.math.ucla.edu/~tao/blue.html

This question was created by mathematician Terence Tao.

Answer 34

0.(9)=1

Answer 35

For quite a while, when I was very young, I thought that the solution to the famed brachistochrone problem (which asks about the shape of a wire where a bead sliding frictionlessly on it under the influence of gravity will take the least amount of time to finish) was not a straight line was pretty counterintuitive, after being repeatedly told that the straight line is the shortest path between two points. (To spoil: the true brachistochrone is an inverted cycloid, which is the curve traced by a fixed point on the rim of a rolling circle.) I went through the derivation a number of times before finally being convinced.

Answer 36

Seat $n$ dining people at a round table. Is it possible to re-seat these people $n-2$ times during that dinner so that at the end everybody has been seated to the left of everybody else?

Intuition suggests that this works (at least) for $n$ prime. I find it highly counterintuitive that this is possible if and only if $n \not\in \{4,6\}$. This is a special case of the Oberwolfach problem, see also this answer by Ben.

Answer 37

I find it counterintuitive that the rational numbers have zero measure. This means that for any $\epsilon$, no matter how small, we can find a collection of intervals that includes every rational but whose total length is less than $\epsilon$.

Such a covering includes all the rationals, but somehow must omit nearly all the irrationals. The question has some up here several times about what irrationals are missed (1 2 3), and Asaf Karagila recently described the result as “baffling”. So I am not the only person who is surprised by this.

Von Neumann famously said that in mathematics you don't understand things, you just get used to them. This for me is one of those things.

(The countability of the rationals, or the uncountability of the irrationals, may be similarly baffling, but I have gotten so used to both that I no longer find either one baffling, and I am not sure which one should be considered counterintuitive.)

Answer 38

It's fairly straightforward to prove that the Cantor set is uncountably infinite (i.e. it has the same cardinality as the real numbers). You would think that such a set would have at least positive Lebesgue measure. WRONG-IT ACTUALLY HAS MEASURE ZERO! This blew my mind when I first learned about in undergraduate real analysis and it's why it puzzles me why Paul Halmos famously described measure theory as "a generalized kind of counting". This example seems to show that measure has nothing to do with cardinality, which is what most of us think of as counting in abstract sets!

Answer 39

I always found the main correspondence of class field theory counter-intuitive. Somehow the (Abelian) field extensions of a number field $K$ correspond to arithmetic objects in $K$ itself.

You wouldn't think that the possible ways of extending a field (albeit in a nice way) would just depend on the field you started with.

Answer 40

I am surprised nobody has given this example: It was once thought that continuous functions have derivatives at almost all points (as other answerers have used). Then comes the Brownian motion model that generates a random curve, which, with probability 1, is a curve without derivative at any points!

Answer 41

Sporadic simple groups in the Classification of finite simple groups

https://en.wikipedia.org/wiki/Classification_of_finite_simple_groups

I find the existence of the sporadic simple groups https://en.wikipedia.org/wiki/Sporadic_group like the Monster group is pretty astounding considering how simple the definition of group is.

To top things off, I've been told that this group has applications in String Theory through the Monstrous Moonshine, although my Mathematics is not advanced enough to appreciate that one yet ;-)

I have explained some of the most basic definitions you need to understand the statement of this theorem at: Intuition behind normal subgroups

The relationship between the sporadic simple groups is also pretty cool:

Image source.

Twin prime conjecture and its variants

https://en.wikipedia.org/wiki/Twin_prime

According to the prime number theorem primes get less and less common. This is of course obvious as we have more and more earlier primes sieving them.

One might therefore consider it possibly surprising that there are likely infinitely many twin primes. This is yet unproven in 2023, but we have an upper bound of 246 now by Zhang and Polymath project.

This might be considered less surprising if you believe that the primes are truly randomly distributed in some sense, but still.

Answer 42

Independence in Statistics. If I have a box with red & black socks, and I take one, and then another one the probability of both socks being red is sometimes different from the case when I, instead, pick a pair. (EX.If all socks are connected to every other with a string, like a complete graph, and then I pick some string, automatically choosing the socks at either end as the pair selected).

Answer 43

Set theory dealing with infinite sets is full of counterintuitive stuff, but comparing Cantor's diagonal argument (which proves [0,1] is uncountable; and is indicative of a common technique for showing the uncountability of an infinite set) to the ordinal numbers and the fact that there is a first uncountable ordinal (provable without the axiom of choice) is profoundly bewildering, even to someone well versed in both constructions.

Answer 44

The St. Petersburg's Paradox was counter-intuitive enough for me to change how I think of $\infty$.

Suppose you start with \$1 and a coin flip. If the coin lands tails, you take all your winnings (\$1 at this point) and the game ends. If it is heads, you get you double your winnings and get to continue flipping. Each heads doubles your winnings until you get a tails which ends the game. Question: what's the average winnings from this game?

The answer is (you guessed it since I spoiled it) $\infty$. It's quite easy to show:

$\mathbb{E}[\text{winnings}] = \sum_{k = 1}^{ \infty } (1/2)^k 2^{k-1} = \infty$

But notice that with probability 1, you will always get a finite amount! So how is the average value of something that is finite with probability 1 infinite?!?

If you think of $\infty$ as number, this seems to make no sense. The average of a set of values cannot be larger than all of the values. But if you think of $\infty$ as simply meaning "without an upper limit", it does seem to make sense. That is, if one were to set a fixed price to play this game, for any fixed (and thus finite) price, if this game is played enough, the average return will exceed that finite price.

Answer 45

Some of us may find it uncomfortable to accept that the "size" of set of all rational numbers and "size" of all integers are the same. Another example is that the "size" of set of all points on a line segment and "size" of set of all points on a line is the same.