I deleted a previous attempt using a approach with the single lead compensator and provide this alternative solution below.
The root locus shows all closed loop pole locations, which follow the root locus trajectories as the loop gain is adjusted. From that we can choose closed loop pole locations that meet our requirements for settling time, loop bandwidth, stability etc. In general the dominant poles will set the loop characteristics such that we can ignore all "weaker" poles. Dominant poles are the ones closes to the imaginary axis (in the left half plane specifically for stability). This is because the impulse response decays faster as the pole is further from to the imaginary axis (consider that a real pole at $s = -x$ has an impulse response given by $e^{-xt}$), so if one pole is significantly closer, it will be continuing to decay long after the further pole has mostly diminished.
Here is the root locus for the OP's plant prior to any compensation. All open loop poles will terminate in the open loop zeros as the loop gain is increased, and the open loop zeros never change, becoming the closed loop zeros. Since there are more finite poles than finite zeros (as a proper system), there is an additional zero at infinity. So we see the two dominant open loop poles at $s=-0.22$ start out going up and down in the positive and negative imaginary direction, circle around and meet in the right half plane where one turns and terminates on the zero at $s=0.012$ while the other terminates in the zero at $s = +18$) (off the plot to the right). The other pole at $s=-45$ terminates in the zero shown at $s=-1.05$ while the remaining pole at $s=-1000$ terminates in the zero at infinity going in the direction of the negative real axis.
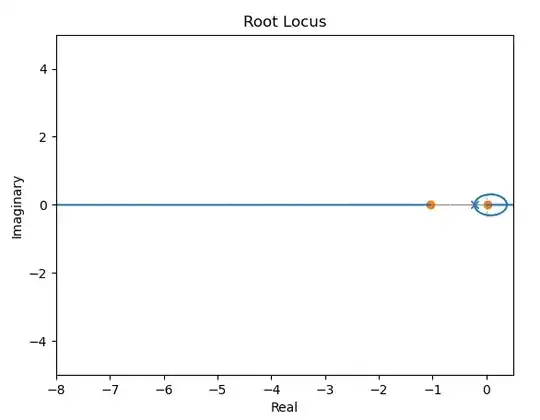
Here is the resulting root locus after using a compensator that uses two zeros at $s=-.22$ to cancel the two dominant poles and then a pole at $s= -1.05$ to cancel that low frequency zero and one more pole at $s= -2$ to terminate in the zeros in the right half plane (that can't be cancelled). With a loop gain of 0.1164 the damping factor is 0.93 which provides for fastest rise time while keeping a reasonable overshoot (the distance from the real axis is the natural frequency while the distance from the imaginary axis is the decay time as previously described; by increasing the natural frequency we introduce some ringing into the loop but it will increase the rise/fall time by getting to the target level quicker--if we overdue that then we get excessive ringing/overshoot which is not desirable).

With the resulting comparative step response (this has a very large negative excursion but will be fully settled in less than the 3 seconds desired by the OP:

This solution using pole-zero cancellation will be very sensitive to the accuracy of the cancellation; any small error will result in a residual transient that will take a long time to settle.


