You can employ Compressed Sensing / Sparse Representation for Super Resolution in Frequency Domain.
One way to do so is solving the problem:
$$ \arg \min_{\boldsymbol{x}} \frac{1}{2} {\left\| F \boldsymbol{x} - \boldsymbol{y} \right\|}_{2}^{2} + \lambda {\left\| \boldsymbol{x} \right\|}_{1} $$
Where the $ {L}_{1} $ norm is sparsity inducing regularization and $ F $ is the inverse DFT matrix.
Solving this, quite simple, optimization problem will yield Super Resolution of the DFT.
Super Resolution means, in that context, being able to resolve frequencies which are closer than what the observation time suggests:
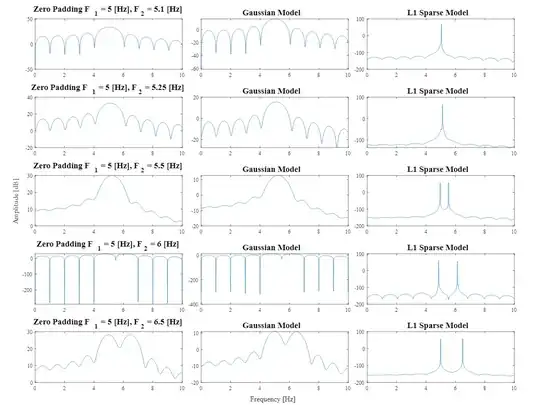
In the above you can see the DFT of a sum of 2 sines with the given frequencies. The Gaussian model is using $ {L}_{2} $ for regularization (Which is basically damped zero padding).
You may see that the $ {L}_{1} $ could resolve the 2 sines even when they are only 0.5 [Hz] apart with an observation windows of 1 [Sec].
This is pretty nice...
