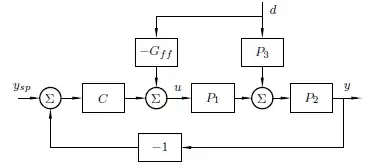
The reference Feedforward control concepts through Interactive Tools says, to minimise the effect of the disturbance $d$ on the process output $y$, a compensator $G_{\text{ff}}=P_3/P_1$ shall be used. From a theory point of view, no problem. Even a few simple examples behave as expected.
Encouraged by that, I decided to implement three-phase inverter control in $dq$ reference frame. Inverter model is represented by LC filter equations:
$$
\text{L} \frac{\operatorname{d}}{\operatorname{d}t}
\begin{bmatrix}
i_\text{d} \\
i_\text{q} \\
\end{bmatrix} =
\begin{bmatrix}
v_\text{dn} \\
v_\text{qn} \\
\end{bmatrix} -
\begin{bmatrix}
v_{\text{d load}} \\
v_{\text{q load}} \\
\end{bmatrix} + \text{L} \omega
\begin{bmatrix}
i_\text{q} \\
-i_\text{d} \\
\end{bmatrix}
$$
$$
\text{C} \frac{\operatorname{d}}{\operatorname{d}t}
\begin{bmatrix}
v_\text{d load} \\
v_\text{q load} \\
\end{bmatrix} =
\begin{bmatrix}
i_\text{d} \\
i_\text{q} \\
\end{bmatrix} -
\begin{bmatrix}
i_{\text{d load}} \\
i_{\text{q load}} \\
\end{bmatrix} + \text{C} \omega
\begin{bmatrix}
v_\text{q load} \\
-v_\text{d load} \\
\end{bmatrix}
$$
From there, I derive plant model and control structure in $dq$ reference frame (only $d$ frame is shown):

In this case disturbance $i_{\text{d load}}$ is fed directly to the plant model. i.e. $P_3=1$. Open-loop inner loop equation is: $$ G_\text{co}(s) = \underbrace{K_\text{P} \left( 1 + \frac{1}{s T_\text{I}} \right)} _\text{PI controller} \underbrace{ \left(\frac{1}{s \text{L}}\right) } _{\text{Process}} $$ and closed loop ($P_1$) is $$ G_\text{cc}(s) = \frac{G_\text{co}(s)}{1 + G_\text{co}(s)} = ... = \frac{s T_\text{I}+1}{s^2 \text{L} T_\text{I}/K_\text{P} + s T_\text{I} + 1} $$ Compensator transfer fucntion is $G_{\text{ff}}=1/G_\text{cc}(s)$ and numerator is a higher order than the denominator.
- I cannot implement this transfer function in MATLAB Simulink. Is there a way forward?
- I don't see any issues with the method! Is this the right approach? Articles deal little with feed-forward signal or cross-coupling compensation.
- When I make $P_3$ equal to $P_1$, i.e. $G_{\text{ff}}=1$, the disturbance is eliminated. In other cases, there is a huge overshoot for step disturbance. It eventually stabilises.
- I also have to compensate the cross-coupling element $\omega\text{C}v_{\text{q load}}$ using the same compensator?
- In the real system (e.g. DSP), I will implement only the control part in $dq$ frame. Do I need to add compensators to load current and cross-coupling signals? Also, the plant's transfer function will be different and unknown. How to determine compensator there or leave it at 1 and only tune PI controller to get the desired response.