This is nice question which I have recently encountered while studying ideal filters. Suppose transfer function $H(p)$ which is complex rational and holomorphic (or meromorphic?) in $p = \sigma + j\omega$ and satisfy Cauchy-Riemann conditions.
We can rewrite transfer function as $H(p) = e^{-\Gamma(p)}=10^{-\frac{1}{20}\Gamma(p)}$ with respect to nepers and decibels. Since exponetital function is holomorphic so the $\Gamma$ is. If we restrict ourselves to imaginary axis $p = j\omega$ we have
$\Gamma(j\omega) = A(j\omega) + jB(j\omega)$
where $A(j\omega)$ is an attentuation charateristics and $B(j\omega)$ is a phase characteristics.
In general we have identity $\ln z = \ln |z| + j\arg z$ for any $z \in \mathbb{C}$. So we can write
$A(j\omega) = \ln|H(j\omega)|$ and $B(j\omega)=\arg H(j\omega)=\arctan\frac{\Im\lbrace H(j\omega)\rbrace}{\Re\lbrace H(j\omega)\rbrace} $.
Then consider pair of Hilbert transforms given by integrals (Cauchy principal value are taken in each of the integrals)
\begin{equation}
A(\omega) = \frac{1}{\pi}\int_{-\infty}^{\infty}\frac{B(j\xi)}{\omega - \xi}\,\mathrm{d}\xi \quad\quad B(\omega) = -\frac{1}{\pi}\int_{-\infty}^{\infty}\frac{A(j\xi)}{\omega - \xi}\,\mathrm{d}\xi
\end{equation}
Evaluating these integrals for module characteristic of ideal low pass filter - say let $A(\omega)$ is constant at $a$ from $-\omega_1$ to $\omega_1$ (module characteristics are symetric) gives
\begin{equation}
B(\omega) = - \frac{a}{\pi}\ln\frac{|\omega + \omega_1|}{|\omega - \omega_1|}
\end{equation}
Thus $B(\omega)$ has points in infinity at $\pm\omega_1$.
See picture bellow:
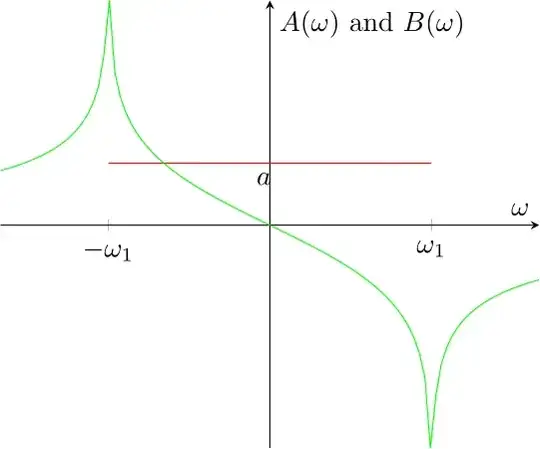
Similarly for linear phase characteristics $B(\omega) = a\omega$.
This is saying to us that we can't reach filter transfer function $H(p)$ with both ideally rectangular module characteristics and ideally linear phase characteristics at the same time.
We see that $B(\omega)$ with points at $\pm \infty$ can't realise any phase characteristics $\arg H(j\omega)$ of a given feasible filter. That's the reason why
\begin{equation}
-\frac{1}{\pi}\int_{-\infty}^{\infty}\frac{A(j\xi)}{\omega - \xi}\,\mathrm{d}\xi < \infty
\end{equation}
must converge and so the
\begin{equation}
-\frac{1}{\pi}\int_{-\infty}^{\infty}\frac{|A(j\xi)|}{\omega^2 + \xi^2}\,\mathrm{d}\xi < \infty
\end{equation}
must.
