Capacity of AWGN channel

Question

I am confused understanding basic concepts of communication over AWGN channels. I know the capacity of a discrete time AWGN channel is: $$C=\frac{1}{2}\log_2\left(1+\frac{S}{N}\right)$$ and it is achieved when the input signal has Gaussian distribution.

• But, what does it mean that the input signal is Gaussian? Does it mean that the amplitude of each symbol of a codeword must be taken from a Gaussian ensemble?
• What is the difference between using a special codebook (in this case Gaussian) and modulating the signal with M-ary signaling, say MPSK?

Answer 1

Assuming a channel whose input at each time is a continuous random variable $X$ and its output is $Y=X+Z$, where $Z\sim\mathcal{N}(0,N)$ and $Z$ is independent of $X$, then $$C_{\text{CI-AWGN}}=\frac{1}{2}\log_2\left(1+\frac{P}{N}\right)$$ is the capacity of the continuous-input channel under the power constraint $$\mathsf{E}X^2\le P$$ The mutual information $I(X;Y)$ is maximized (and is equal to $C_{\text{CI-AWGN}}$) when $X\sim\mathcal{N}(0,P)$.

This means that if $X$ is a continuous Gaussian random variable with the given variance, then the output has the highest possible mutual information with the input. That's it!

When the input variable $X$ is discretized (quantized), a new formulation is required. Indeed, things can easily become difficult. To see it a little bit, one can consider the simple case of a very coarse discritization of $X$ where it can only have two values. So assume that $X$ is selected from a binary alphabet, for instance let $X\in\{\pm1\}$ (or a scaled version to satisfy a power constraint). In terms of modulation, it is identical to BPSK.

It turns out that the capacity (even in this simple case) has no closed form. I report from "Modern Coding Theory" by Richardson and Urbanke:

$$\begin{align}C&_{\text{BI-AWGN}}=1+\\&\frac{1}{\ln(2)} \left(\left(\frac{2}{N}-1\right)\mathcal{Q}\left(\frac{1}{\sqrt{N}}\right)-\sqrt{\frac{2}{\pi N}}e^{-\frac{1}{2N}}+\sum_{i=1}^{\infty}\frac{(-1)^i}{i(i+1)}e^{\frac{2i(i+1)}{N}}\mathcal{Q}\left(\frac{1+2i}{\sqrt{N}}\right)\right)\end{align}$$ A comparison between the two cases can be seen in the figure below:

Answer 2

The capacity formula $$C = 0.5 \log (1+\frac{S}{N}) \tag{1}$$ is for discrete time channel.

Assuming you have a sequence of data $\left\lbrace a_n \right\rbrace$ to send out, you need an orthonormal waveform set $\left\lbrace \phi_n(t) \right\rbrace$ for modulation. In linear modulation, whom M-ary modution belongs to, $\phi_n(t) = \phi(t - nT)$ where $T$ is symbol duration and $\phi(t)$ is prototype waveform so that the baseband continous time TX signal becomes $$x(t) = \sum_n a_n \phi(t-nT) \tag{2}$$

Typical modulations use the special case that $\left\lbrace \phi_n(t) \right\rbrace$ satisfies the Nyquist ISI criterion with matched filter to recover $a_n$. A well-known $\phi(t)$ is Root raised cosine.

The continuous AWGN channel is a model that $$y(t) = x(t) + n(t) \tag{3}$$

where $n(t)$ is a Gaussian white stochastic process.

From (2), we can see that $a_n$ is the projection of $x(t)$ on $\left\lbrace \phi_n(t) \right\rbrace$. Do the same thing with $n(t)$, the projections of $n(t)$ on an orthonormal set is a sequence of iid Gaussian random variables $w_n = \langle n(t),\phi_n(t) \rangle$ (I really think that $n(t)$ is defined from its projections); and call $y_n = \langle y(t),\phi_n(t) \rangle$. Voilà, we have an equivalent discrete time model $$y_n = a_n + w_n \tag{4}$$

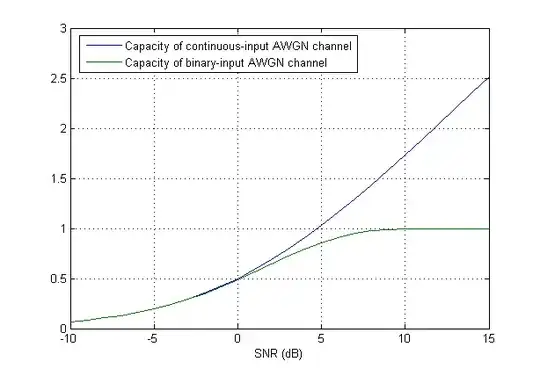
The formula (1) is stated for $S$ and $N$ are energy (variance if $a_n$ and $w_n$ are zero mean) of $a_n$ and $w_n$, respectively. If $a_n$ and $w_n$ are Gaussian, so is $y_n$ and the capacity is maximized. (I can add a simple proof if you want).

what does it mean that the input signal is Gaussian? Does it mean that the amplitude of each symbol of a codeword must be taken from a Gaussian ensemble?

It mean random variables $a_n$ are Gaussian.

What is the difference between using a special codebook (in this case Gaussian) and modulating the signal with M-ary signaling, say MPSK?

The waveform $\phi_n(t)$ set needs to be orthonormal, which is true for M-PSK, so that $w_n$ is iid Gaussian.

Update However $a_n$ is quantized so in general, it is not Gaussian anymore. There is some researchs about this topic, such as usage of Lattice Gaussian Coding (link).

Answer 3

To say that the input signal has a Gaussian distribution means that it is distributed as a Gaussian random variable. In practice, one relies on coding over multiple instances of the channel (in time) instead of relying on a Gaussian input distribution. There is a beautiful theory full of proofs that is beyond the scope of this answer (Information Theory). Error control codes (or channel codes) typically rely on the use of familiar QAM/PSK modulations, but through the redundancy of the code and multiple channel uses, they can approach (though not quite reach) the channel capacity. A sketch of the reasoning (without full details) is provided next.

The definition of channel capacity is $$ C = \sup_{p_X(x)} I(X; Y)$$ where $X$ can loosely be referred to as your input random variable, and $Y$ can loosely be referred to as your output random variable, and $I(\cdot,\cdot)$ is the Mutual Information of $X$ and $Y$. This definition requires us to search over all possible distributions of the input $p_X(x)$ for distributions that maximize the Mutual Information. The discrete AWGN channel has an input/output relationship defined as $$ Y = X + Z $$ where $Z$ is a zero mean Gaussian with variance $\sigma_Z^2$ (notice that $\sigma_Z^2=N$ and $\sigma_X^2=S$ in your notation). I don't have time to provide all of the details right now. However, any book on information theory can walk you through the proof that shows that if $X$ is distributed as a Gaussian then $I(X;Y)$ (the mutual information of $X$ and $Y$) is maximized. For example, see Elements of Information Theory by Thomas Cover. If you haven't read it yet, Shannon's original treatise A Mathematical Theory of Communication is a worthwhile read with clear reasoning throughout.