I have a discrete signal $x[n]$ of length say $1024$, such that :
$$-1 \leq x[n] \leq 1, \qquad \forall n$$
and let $y[k]$ be its DFT.
Is there an upper bound for $|y[k]|$ ? (i.e. for the DFT of a bounded signal)
Asked
Active
Viewed 611 times
3 Answers
6
You can obtain a bound on the magnitude of the DFT of $x[n]$ ($|x[n]|\le 1$) as follows:
$$\big|X[k]\big|=\left|\sum_{n=0}^{N-1}x[n]e^{-jkn2\pi/N}\right|\le\sum_{n=0}^{N-1}|x[n]|\le N\max_n|x[n]|=N\tag{1}$$
Note that for signals $x[n]=e^{j2\pi nl/N}$, $l\in\mathbb{Z}$, the bound is tight. However, for most other signals with $|x[n]|\le 1$ you will find that the maximum of $|X[k]|$ is substantially smaller than the bound given by $(1)$.
Matt L.
- 78,282
- 5
- 66
- 149
-
Can we exhibit an example of sequence $x[n]$ such that one $|y[k]|$ is close to $N$ ? – Basj May 11 '14 at 21:46
-
@Basj: For some frequency index $k$ let $x[n]=e^{jkn2\pi/N}$. – Matt L. May 12 '14 at 06:13
-
@Basj: Just take the sinusoid. – jojek May 12 '14 at 07:30
-
@MattL. I already upvoted – Basj May 12 '14 at 09:26
-
I don't understand why you are saying the bound is not tight since there is at least one instance of a signal that meets it with equallty. Any "tighter" bound for signals meeting the stated criteria would not be satisfied by the signals that meet the "looser" bound that you specify. – Dilip Sarwate Sep 10 '18 at 11:51
-
@DilipSarwate: You're right that the bound is tight in that sense. What I meant was that for a randomly chosen signal $x[n]$ satisfying $|x[n]|\le 1$ the bound might be quite loose. I'll edit my answer accordingly. – Matt L. Sep 10 '18 at 11:56
-
@DilipSarwate, what is that instance? the only one i can think of is: $$ x[n] = e^{j 2 \pi kn/N} $$ and that is *"tight"* only for a single value of $k$. – robert bristow-johnson Sep 11 '18 at 00:45
-
@robertbristow-johnson There are $N$ different sequences $x_k[n] = \exp(2\pi kn/N)$ that meet the requirement of being bounded in $[-1,1]$, and each has the property that the maximum magnitude of _some_ DFT coefficient is $N$. So what if only one of the DFT coefficients has value $N$ (and the others have value $0$)??? The question is how large can the maximum value of a DFT coefficient be? It is not asking for how large the average magnitude can be or anything like that. If one DFT coefficient is large and the others are small, so be it; the small fry don't matter. – Dilip Sarwate Sep 11 '18 at 01:32
5
The upper bound would be a coherent summation of all samples of $ x \left [ x \right ] $.
Specifically:
$$\begin{aligned} X \left[ k \right ] & = \sum_{n = 0}^{N - 1} x \left[ n \right] \exp^{-j 2 \pi \frac{nk}{N}} \\ & \leq \left| \sum_{n = 0}^{N - 1} x \left[ n \right] \exp^{-j 2 \pi \frac{nk}{N}} \right| \\ & \leq \sum_{n = 0}^{N - 1} \left| x \left[ n \right] \exp^{-j 2 \pi \frac{nk}{N}} \right| \\ & \leq \sum_{n = 0}^{N - 1} \left| x \left[ n \right] \right| \\ & \leq N \max_{n} \left \{ \left| x \left[ n \right] \right| \right \} \end{aligned}$$
If you add the info $ \forall n \left| x \left[ n \right] \right| \leq 1 $ you can say you're bounded by $ N $.
I hope this helps...
Royi
- 33,983
- 4
- 72
- 179
1
All calculated coefficients of your FFT will be lower than maximum amplitude of your signal. Of course I mean normalized FFT, you must divide each of them by length of your sequence (in case of rectangular window). Two cases you should think of are:
One sinusoid varying between $-1$ and $1$ produces obviously peak in spectrum at its frequency with amplitude of $1$. That's what we expect
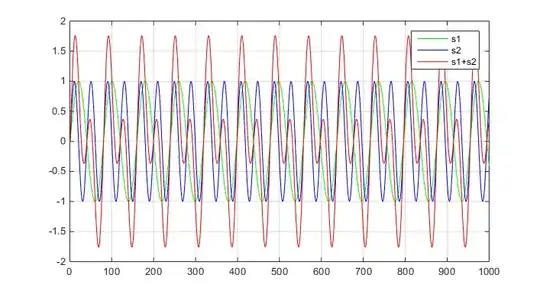
You have two (or more) sinusoids, each of them has also unit amplitude. Their superposition might produce signal (your signal $x[n]$ ) with an amplitude higher than $1$. You can observe that on plot below. Although when you do the FFT you will get two separated peaks with amplitude $1$. That means you cannot get signal with spectral peak values higher than time domain amplitude.
In some cases you will also encounter leakage problem, and the amplitude of your peak will be bit lower than it should be. But this also assures that you won't get more than maximum absolute value in the time domain.
jojek
- 10,340
- 6
- 32
- 71