My knowledge of wavelets is less than epsilon. Bear with me. If I have a signal of two well separated sinusoids (15 and 48 Hz) plus some random noise, I can clearly make out the two in a spectrogram (the two stripes in my picture);
t=0:0.002:1; % fs = 500 Hz
x=4*sin(2*pi*15*t)+2*cos(2*pi*48*t);
xn = x + randn(size(x));
figure(1);
plot(xn);
figure(2);
spectrogram(xn, 64, 60, [], 500);

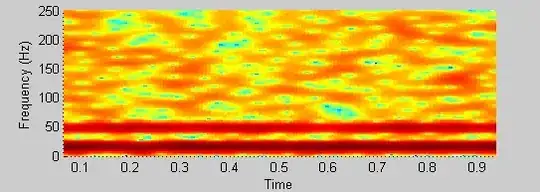
but, using 'wscalogram', I cant say I can tell the components apart:
coefs = cwt(xn,1:64,'db8','scalCNT');
wscalogram('image',coefs,'scales',1:64,'ydata',xn);
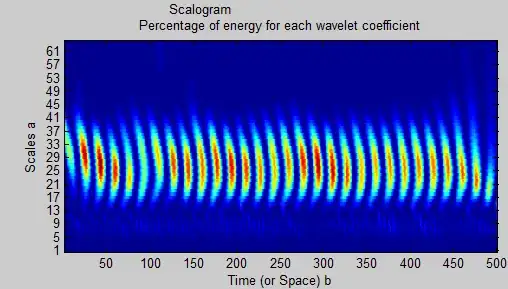
Is there a way to read from the scalogram that there are 2 distinct sinusoids and if so, how can I separate them using wavelet decomposition and filtering? I thought that perhaps my choice of wavelet ('db8') is not optimal but I can't see much difference using other types ad larger (or smaller) number of scales. Clearly I am missing something about where and when and on what to apply wavelets.
Thanks
